河南省洛阳市汝阳县2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-12-15 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、﹣3 B、3 C、﹣9 D、92. 用配方法解方程x2+3=4x,配方后的方程变为( )A、(x-2)2=7 B、(x+2)2=1 C、(x-2)2=1 D、(x+2)2=23. 在 中, =90〫, ,则 的值是( )A、 B、 C、 D、4. 一块矩形菜地的面积是120平方米,如果它的长减少2米,菜地就变成正方形,则原菜地的长是( )A、10 B、12 C、13 D、145. 将抛物线 向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析是( )A、 B、 C、 D、6. 如图,DE∥BC,BD,CE相交于O, , ,则 ( ).
 A、6 B、9 C、12 D、157. 已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为 ,则a等于( )A、1 B、2 C、3 D、48. 已知点 、 、 在函数 上,则 、 、 的大小关系是( ).(用“>”连结起来)A、 B、 C、 D、9. 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα= , 则“人字梯”的顶端离地面的高度AD是( )
A、6 B、9 C、12 D、157. 已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为 ,则a等于( )A、1 B、2 C、3 D、48. 已知点 、 、 在函数 上,则 、 、 的大小关系是( ).(用“>”连结起来)A、 B、 C、 D、9. 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα= , 则“人字梯”的顶端离地面的高度AD是( )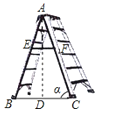 A、144cm B、180cm C、240cm D、360cm10. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
A、144cm B、180cm C、240cm D、360cm10. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )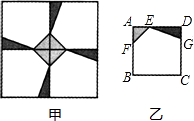 A、
A、 B、
B、 C、
C、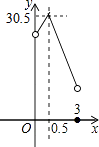 D、
D、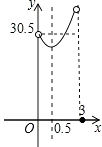
二、填空题
-
11. 计算: = .12. 河堤横截面如图所示,堤高 为4米,迎水坡 的坡比为1: (坡比= ),那么 的长度为米.
 13. 一个口袋中装有2个完全相同的小球,它们分别标有数字1,2,从口袋中随机摸出一个小球记下数字后放回,摇匀后再随机摸出一个小球,则两次摸出小球的数字和为偶数的概率是 .
13. 一个口袋中装有2个完全相同的小球,它们分别标有数字1,2,从口袋中随机摸出一个小球记下数字后放回,摇匀后再随机摸出一个小球,则两次摸出小球的数字和为偶数的概率是 .
14. 将一副三角尺如图所示叠放在一起,则的值是 .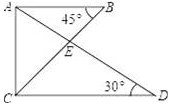
15. 已知如图, 是 的中位线,点 是 的中点, 的延长线交 于点 ,那么 =.
三、解答题
-
16. 计算:17. 某中学现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学代表学校参加全市汉字听写大赛.(1)、请用树状图或列表法列举出各种可能选派的结果;(2)、求恰好选派一男一女两位同学参赛的概率.18. 某批发商以每件50元的价格购500件 恤,若以单价70元销售,预计可售出200件,批发商的销售策略是:第一个月为了增加销售,在单价70元的基础上降价销售,经过市场调查,单价每降低1元,可多售出10件,但最低单价高于购进的价格,每一个月结束后,将剩余的 恤一次性亏本清仓销售,清仓时单价为40元.(1)、若设第一个月单价降低 元,当月出售 恤获得的利润为 元,清仓剩下 恤亏本 元,请分别求出 、 与 的函数关系式;(2)、从增加销售量的角度看,第一个月批发商降价多少元时,销售完这批 恤获得的利润为1000元?19. 已知关于x的一元二次方程(a+c)x2+2bx+a-c=0,其中a、b、c分别为△ABC三边的长.(1)、若方程有两个相等的实数根,试判断△ABC的形状,并说明理由;(2)、若△ABC是正三角形,试求这个一元二次方程的根.20. 小王同学在地质广场上放风筝,如图风筝从 处起飞,几分钟后便飞达 处,此时,在 延长线上 处的小张同学发现自己的位置与风筝和广场边旗杆 的顶点 在同一直线上,已知旗杆高为10米,若在 处测得旗杆顶点 的仰角为30〫, 处测得点 的仰角为45〫,若在 处背向旗杆又测得风筝的仰角为75〫,绳子在空中视为一条线段,求绳子 为多少米?(结果保留根号)
 21. 已知二次函数 的图象经过点 .
21. 已知二次函数 的图象经过点 . (1)、求这个函数的解析式;(2)、画出它的简图,并指出图象的顶点坐标;(3)、结合图象直接写出使 的 的取值范围.22. 如图1,已知直线 ,线段 在直线 上, 于点 ,且 , 是线段 上异于两端点的一点,过点 的直线分别交 、 于点 、 (点 、 位于点 的两侧),满足 ,连接 、 .
(1)、求这个函数的解析式;(2)、画出它的简图,并指出图象的顶点坐标;(3)、结合图象直接写出使 的 的取值范围.22. 如图1,已知直线 ,线段 在直线 上, 于点 ,且 , 是线段 上异于两端点的一点,过点 的直线分别交 、 于点 、 (点 、 位于点 的两侧),满足 ,连接 、 . (1)、求证: ;(2)、连结 、 , 与 相交于点 ,如图2,
(1)、求证: ;(2)、连结 、 , 与 相交于点 ,如图2,①当 时,求证: ;
②当 时,设 的面积为 , 的面积为 , 的面积为 ,求 的值.
23. 如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.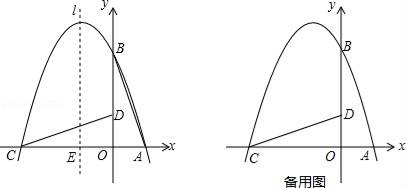 (1)、求抛物线的解析式;(2)、若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.
(1)、求抛物线的解析式;(2)、若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.