初中数学苏科版八年级上学期期末复习专题(4) 线段、角的轴对称性
试卷更新日期:2020-12-15 类型:复习试卷
一、单选题
-
1. 若P是△ 所在平面内的点,且 ,则下列说法正确的是( )A、点P是△ 三边垂直平分线的交点 B、点P是△ 三条角平分线的交点 C、点P是△ 三边上高的交点 D、点P是△ 三边中线的交点2. 如图,在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N,若BM=2,CN=3,则MN的长为( )
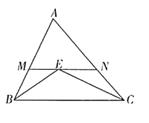 A、10 B、5.5 C、6 D、53. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=12,则点P到BC的距离是( )
A、10 B、5.5 C、6 D、53. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=12,则点P到BC的距离是( ) A、8 B、6 C、4 D、24. 如图,在△ABC中,∠BAC的平分线AD和边BC的垂直平分线ED相交于点D , 过点D作DF垂直于AC交AC的延长线于点F , 若AB=8,AC=5,则CF=( )
A、8 B、6 C、4 D、24. 如图,在△ABC中,∠BAC的平分线AD和边BC的垂直平分线ED相交于点D , 过点D作DF垂直于AC交AC的延长线于点F , 若AB=8,AC=5,则CF=( )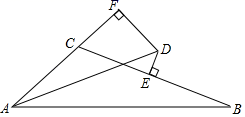 A、1.5 B、2 C、2.5 D、35. 如图,四边形ABCD中,∠A=90°,AD=2,连接BD , BD⊥CD , 垂足是D且∠ADB=∠C , 点P是边BC上的一动点,则DP的最小值是( )
A、1.5 B、2 C、2.5 D、35. 如图,四边形ABCD中,∠A=90°,AD=2,连接BD , BD⊥CD , 垂足是D且∠ADB=∠C , 点P是边BC上的一动点,则DP的最小值是( )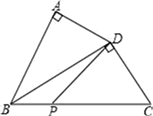 A、1 B、1.5 C、2 D、2.56. 如图, 是 的角平分线,点 是 上一点,作线段 的垂直平分线交 于点 ,交 于点 ,过点 作 交 于点 ,连接 ,若 , .则 的面积为( )
A、1 B、1.5 C、2 D、2.56. 如图, 是 的角平分线,点 是 上一点,作线段 的垂直平分线交 于点 ,交 于点 ,过点 作 交 于点 ,连接 ,若 , .则 的面积为( ) A、 B、 C、 D、7. 如图,AE平分△ABC外角∠CAD,且AE∥BC,给出下列结论:①∠DAE=∠CAE;②∠DAE=∠B;③∠CAE=∠C;④∠B=∠C;⑤∠C+∠BAE=180°,其中正确的个数有( )
A、 B、 C、 D、7. 如图,AE平分△ABC外角∠CAD,且AE∥BC,给出下列结论:①∠DAE=∠CAE;②∠DAE=∠B;③∠CAE=∠C;④∠B=∠C;⑤∠C+∠BAE=180°,其中正确的个数有( )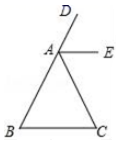 A、5个 B、4个 C、3个 D、2个8. 如图,在 中, , 平分 交 于点D, 于点E,下列结论中正确的个数是( ).
A、5个 B、4个 C、3个 D、2个8. 如图,在 中, , 平分 交 于点D, 于点E,下列结论中正确的个数是( ).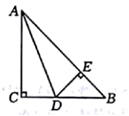
① 平分 :② ;③ 平分 ;④ .
A、3个 B、2个 C、1个 D、4个9. 如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1 , 得∠A1;∠A1BC与∠A1CD的平分线相交于点A2 , 得∠A2;……:∠An-1BC与∠An-1CD的平分线交于点An , 要使∠An的度数为整数,则n的最大值为( ) A、4 B、5 C、6 D、710. 如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( )
A、4 B、5 C、6 D、710. 如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
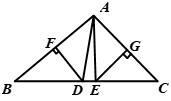
11. 如图,在△ABC中,∠B=38°,∠C=40°,AB的垂直平分线交BC于D , AC的垂直平分线交BC于E , 则∠DAE= ° .
 12. 在直角△ABC中,已知∠ACB=90°,AB=13,AC=12,BC=5.在△ABC的内部找一点P,使得P到△ACB的三边的距离相等,则这个距离是.13. 如图,ΔABC的三边AB,BC,CA的长分别为20,30,40,其三条角平分线将ΔABC分为三个三角形,则SΔABO:SΔBCO:SΔAOC等于。
12. 在直角△ABC中,已知∠ACB=90°,AB=13,AC=12,BC=5.在△ABC的内部找一点P,使得P到△ACB的三边的距离相等,则这个距离是.13. 如图,ΔABC的三边AB,BC,CA的长分别为20,30,40,其三条角平分线将ΔABC分为三个三角形,则SΔABO:SΔBCO:SΔAOC等于。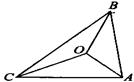 14. 如图,OP平分∠AOB , PM⊥OA于M , 点D在OB上,DH⊥OP于H . 若OD=4,OP=7,PM=3,则DH的长为 .
14. 如图,OP平分∠AOB , PM⊥OA于M , 点D在OB上,DH⊥OP于H . 若OD=4,OP=7,PM=3,则DH的长为 .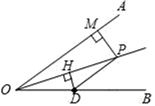 15. 如图,在 中, , 是 的平分线, ⊥ 于点 ,点 在 上, ,若 , ,则 的长为.
15. 如图,在 中, , 是 的平分线, ⊥ 于点 ,点 在 上, ,若 , ,则 的长为. 16. 如图,BD是△ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE的长为
16. 如图,BD是△ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE的长为 17. 如图,等腰三角形 的底边 长为 ,面积是 ,腰 的垂直平分线 分别交 、 于点 、 ,若点 为底边 的中点,点 为线段 上一动点,则 的周长的最小值为.
17. 如图,等腰三角形 的底边 长为 ,面积是 ,腰 的垂直平分线 分别交 、 于点 、 ,若点 为底边 的中点,点 为线段 上一动点,则 的周长的最小值为. 18. 如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于D.过C点作CG⊥AB于G,交AD于E.过D点作DF⊥AB于F.下列结论:①∠CED=∠CDE; ② ;③∠ADF=2∠ECD; ④ ;⑤CE=DF.其中正确结论的序号是.
18. 如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于D.过C点作CG⊥AB于G,交AD于E.过D点作DF⊥AB于F.下列结论:①∠CED=∠CDE; ② ;③∠ADF=2∠ECD; ④ ;⑤CE=DF.其中正确结论的序号是.
三、解答题
-
19. 某地有两条相交叉的公路, 计划修建一个饭馆:希望饭馆点P既在MN这条公路上,又到直线OA、OB的距离相等.你能确定饭馆应该建在什么位置吗?(保留作图痕迹)
 20. 如图, 中,边AB、AC的垂直平分线ED、GF分别交AB、AC于点E、G,交BC于点D、F,连接AD,AF,若 ,求 的度数.
20. 如图, 中,边AB、AC的垂直平分线ED、GF分别交AB、AC于点E、G,交BC于点D、F,连接AD,AF,若 ,求 的度数. 21. 如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,若S△ABD=12,求DF的长.
21. 如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,若S△ABD=12,求DF的长. 22. 已知 的角平分线 与边 的垂直平分线 相交于点 ,作 , ,垂足分别是 、 .求证:
22. 已知 的角平分线 与边 的垂直平分线 相交于点 ,作 , ,垂足分别是 、 .求证: (1)、 .(2)、23. 已知:△ABC中,记∠BAC=α,∠ACB=β.
(1)、 .(2)、23. 已知:△ABC中,记∠BAC=α,∠ACB=β. (1)、如图1,若AP平分∠BAC,BP,CP分别平分△ABC的外角∠CBM和∠BCN,BD⊥AP于点D,用α的代数式表示∠BPC的度数,用β的代数式表示∠PBD的度数.
(1)、如图1,若AP平分∠BAC,BP,CP分别平分△ABC的外角∠CBM和∠BCN,BD⊥AP于点D,用α的代数式表示∠BPC的度数,用β的代数式表示∠PBD的度数.
(2)、如图2,若点P为△ABC的三条内角平分线的交点,BD⊥AP于点D,猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.24. 如图1,△ABC中,点D是BC的中点,BE∥AC,过点D的直线EF交BE于点E,交AC于点F. (1)、求证:BE=CF(2)、如图2,过点D作DG⊥DF交AB于点G,连结GF,请你判断BG+CF与GF的大小关系,并说明理由.25. 如图,在 中, ,BE平分 ,AM BC于点M,AD平分 ,交BC于点D,AM交BE于点G.
(1)、求证:BE=CF(2)、如图2,过点D作DG⊥DF交AB于点G,连结GF,请你判断BG+CF与GF的大小关系,并说明理由.25. 如图,在 中, ,BE平分 ,AM BC于点M,AD平分 ,交BC于点D,AM交BE于点G. (1)、求证: ;(2)、判断直线BE是否垂直平分线段AD,并说明理由.26. 如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.
(1)、求证: ;(2)、判断直线BE是否垂直平分线段AD,并说明理由.26. 如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t. (1)、当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;(2)、当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
(1)、当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;(2)、当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.