2017-2018学年初中数学中考一轮专题复习:一次函数
试卷更新日期:2017-10-11 类型:一轮复习
一、单选题
-
1. 直线y=x+4分别与x轴、y轴相交于点M,N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交于点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )
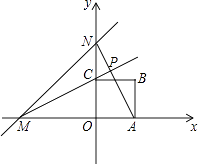 A、2 ﹣2 B、3﹣2 C、 D、12.
A、2 ﹣2 B、3﹣2 C、 D、12.如图,直线y= x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
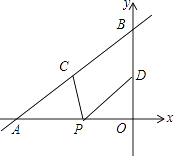 A、(﹣3,0) B、(﹣6,0) C、(﹣ ,0) D、(﹣ ,0)3. 如果一次函数y=kx+b(k、b是常数,k≠0)的图象经过第一、二、四象限,那么k、b应满足的条件是( )A、k>0,且b>0 B、k<0,且b>0 C、k>0,且b<0 D、k<0,且b<04. 把直线y=2x﹣1向左平移1个单位,平移后直线的关系式为( )A、y=2x﹣2 B、y=2x+1 C、y=2x D、y=2x+25. 在同一平面直角坐标系中,直线y=4x+1与直线y=﹣x+b的交点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 在同一平面直角坐标系中,函数y=mx+m(m≠0)与y= (m≠0)的图象可能是( )A、
A、(﹣3,0) B、(﹣6,0) C、(﹣ ,0) D、(﹣ ,0)3. 如果一次函数y=kx+b(k、b是常数,k≠0)的图象经过第一、二、四象限,那么k、b应满足的条件是( )A、k>0,且b>0 B、k<0,且b>0 C、k>0,且b<0 D、k<0,且b<04. 把直线y=2x﹣1向左平移1个单位,平移后直线的关系式为( )A、y=2x﹣2 B、y=2x+1 C、y=2x D、y=2x+25. 在同一平面直角坐标系中,直线y=4x+1与直线y=﹣x+b的交点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 在同一平面直角坐标系中,函数y=mx+m(m≠0)与y= (m≠0)的图象可能是( )A、 B、
B、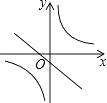 C、
C、 D、
D、 7. 将一次函数y=2x﹣3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( )A、y=2x﹣5 B、y=2x+5 C、y=2x+8 D、y=2x﹣88. 一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )
7. 将一次函数y=2x﹣3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( )A、y=2x﹣5 B、y=2x+5 C、y=2x+8 D、y=2x﹣88. 一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )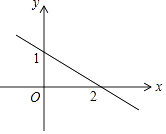 A、x<2 B、x<0 C、x>0 D、x>29. 直线 与y轴的交点坐标是( )A、(4,0) B、(0,4) C、(﹣4,0) D、(0,﹣4)10. 已知方程 解是 ,则直线 与 的交点是( )A、(1,0) B、(1,3) C、(-1,-1) D、(-1,5)11. 已知一次函数的图象与直线 平行,且过点(8,2),那么此一次函数的解析式为( )A、 B、 C、 D、12. 关于一次函数y=﹣2x+3,下列结论正确的是( )A、图象过点(1,﹣1) B、图象经过一、二、三象限 C、y随x的增大而增大 D、当x> 时,y<013.
A、x<2 B、x<0 C、x>0 D、x>29. 直线 与y轴的交点坐标是( )A、(4,0) B、(0,4) C、(﹣4,0) D、(0,﹣4)10. 已知方程 解是 ,则直线 与 的交点是( )A、(1,0) B、(1,3) C、(-1,-1) D、(-1,5)11. 已知一次函数的图象与直线 平行,且过点(8,2),那么此一次函数的解析式为( )A、 B、 C、 D、12. 关于一次函数y=﹣2x+3,下列结论正确的是( )A、图象过点(1,﹣1) B、图象经过一、二、三象限 C、y随x的增大而增大 D、当x> 时,y<013.梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系图象如图所示,则降价后每件商品的销售利润为( )
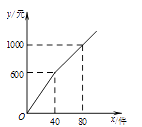 A、4元 B、5元 C、10元 D、15元14. 若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是( )A、k>3 B、0<k≤3 C、0≤k<3 D、0<k<315.
A、4元 B、5元 C、10元 D、15元14. 若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是( )A、k>3 B、0<k≤3 C、0≤k<3 D、0<k<315.如图,直线y=x+b与直线y=kx+6交于点P(1,3),则关于x的不等式x+b>kx+6的解集是( ).
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
16.
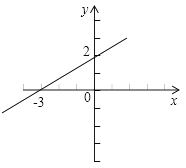
函数y=kx+b的图象如图所示,则当y<0时,x的取值范围是 .
 17. 为了加强公民节水意识,某市制定了如下用水收费标准,每户每月用水不超过10t时,水价为每吨1.2元;超过10t时,超过的部分按每吨1.8元收费,现有某户居民5月份用水xt(x>10),应交水费y元,则y与x的关系式 .18. 点(﹣1,y1)、(2,y2〕是直线y=2x+1上的两点,则y1 y2(填“>”或“=”或“<”).19.
17. 为了加强公民节水意识,某市制定了如下用水收费标准,每户每月用水不超过10t时,水价为每吨1.2元;超过10t时,超过的部分按每吨1.8元收费,现有某户居民5月份用水xt(x>10),应交水费y元,则y与x的关系式 .18. 点(﹣1,y1)、(2,y2〕是直线y=2x+1上的两点,则y1 y2(填“>”或“=”或“<”).19.如图,直线l:y=﹣ x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3 , …,按此做法进行下去,点A2016的坐标为 .
 20. 如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx﹣6<ax+4<kx的解集为 .
20. 如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx﹣6<ax+4<kx的解集为 .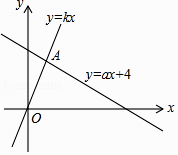 21. 甲、乙两动点分别从线段AB的两端点同时出发,甲从点A出发,向终点B运动,乙从点B出发,向终点A运动.已知线段AB长为90cm,甲的速度为2.5cm/s.设运动时间为x(s),甲、乙两点之间的距离为y(cm),y与x的函数图象如图所示,则图中线段DE所表示的函数关系式为 . (并写出自变量取值范围)
21. 甲、乙两动点分别从线段AB的两端点同时出发,甲从点A出发,向终点B运动,乙从点B出发,向终点A运动.已知线段AB长为90cm,甲的速度为2.5cm/s.设运动时间为x(s),甲、乙两点之间的距离为y(cm),y与x的函数图象如图所示,则图中线段DE所表示的函数关系式为 . (并写出自变量取值范围)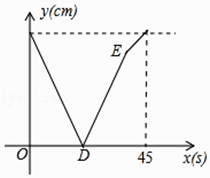 22. 如图,过点(0,3)的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是 .
22. 如图,过点(0,3)的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是 .
三、解答题
-
23.
已知一次函数y=kx+b的图象与x轴、y轴分别交于点A(﹣2,0)、B(0,4),直线l经过点B,并且与直线AB垂直.点P在直线l上,且△ABP是等腰直角三角形.
(1)求直线AB的解析式;
(2)求点P的坐标;
(3)点Q(a,b)在第二象限,且S△QAB=S△PAB .
①用含a的代数式表示b;
②若QA=QB,求点Q的坐标.
 24.
24.如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).求:
(1)求k值与一次函数y=k1x+b的解析式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(3)在y轴上求一点P使△POC为等腰三角形,请求出所有符合条件的点P的坐标.
 25.
25.如图,在矩形ABCO中,点O为坐标原点,点A、C在坐标轴上,点B的坐标为(7,3),点D在y轴上,且D与A关于原点对称,直线
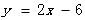 与x轴交于点E,点F(m,-4)在直线
与x轴交于点E,点F(m,-4)在直线 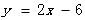 上, 连结DE、DF.
上, 连结DE、DF.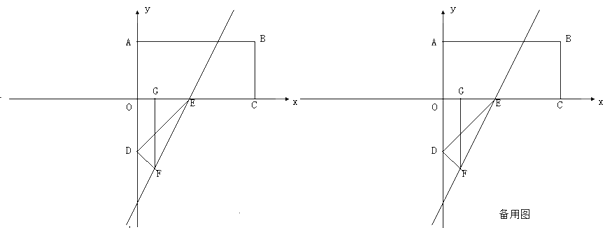 (1)、请直接写出F的坐标和△DEF的形状;答:、 .(2)、若点P在矩形ABCO的边BC上,过F作FG⊥x轴于G.
(1)、请直接写出F的坐标和△DEF的形状;答:、 .(2)、若点P在矩形ABCO的边BC上,过F作FG⊥x轴于G.若线段EF上有一点M,使∠MDF=∠GFE,请求出M的坐标;
(3)、若直线EF上有一点Q,使△APQ是等腰直角三角形,请直接写出满足条件的Q的坐标.答: .
四、综合题
-
26. 直线l的解析式为y=﹣2x+2,分别交x轴、y轴于点A,B.
 (1)、写出A,B两点的坐标,并画出直线l的图象;(2)、将直线l向上平移4个单位得到l1 , l1交x轴于点C.
(1)、写出A,B两点的坐标,并画出直线l的图象;(2)、将直线l向上平移4个单位得到l1 , l1交x轴于点C.①作出l1的图象,
②l1的解析式是 .
(3)、将直线l绕点A顺时针旋转90°得到l2 , l2交l1于点D.①作出l2的图象,
②tan∠CAD= .
27.如图,直线l1:y1=− x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
 (1)、求两直线交点D的坐标;(2)、求△ABD的面积;(3)、根据图象直接写出y1>y2时自变量x的取值范围.28.
(1)、求两直线交点D的坐标;(2)、求△ABD的面积;(3)、根据图象直接写出y1>y2时自变量x的取值范围.28.如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.
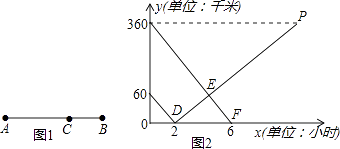 (1)、填空:A,B两地相距千米;(2)、求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;(3)、客、货两车何时相遇?
(1)、填空:A,B两地相距千米;(2)、求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;(3)、客、货两车何时相遇?