2020-2021学年人教版数学六年级上册期末复习14:数学广角——数形结合规律
试卷更新日期:2020-12-14 类型:复习试卷
一、选择题
-
1. 与1+3+5+7+9+5+3+1表示相同结果的算式是( )A、42 B、32 C、52+32 D、52﹣322. 某餐厅里,一张桌子可坐6人,如图所示:

按照上面的规律,n张桌子能坐( )人。
A、6n+4 B、4n+4 C、4n+2 D、6n+63. 如下图,用火柴棒搭房子,搭三间用了13根。照这样计算,搭504间用( )根火柴棒。 A、2013 B、2015 C、20174. 下图是按一定规律连续拼摆制作的图案,按此规律N处的图案应是( )
A、2013 B、2015 C、20174. 下图是按一定规律连续拼摆制作的图案,按此规律N处的图案应是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 笑笑在某月的日历卡上按照下图的方式圈出了三组数(如图所示),他发现每组数中的四个数都有相同的关系,而且用同样的方法再任意圈出四个数,他们的关系不变。下面的四个表达式中,最能表示每组四个数之间的关系的是( )
5. 笑笑在某月的日历卡上按照下图的方式圈出了三组数(如图所示),他发现每组数中的四个数都有相同的关系,而且用同样的方法再任意圈出四个数,他们的关系不变。下面的四个表达式中,最能表示每组四个数之间的关系的是( ) A、
A、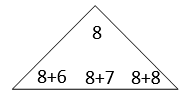 B、
B、 C、
C、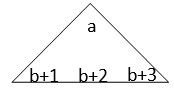 D、
D、 6. 王鹏用小棒摆了四幅树状图,以下是树状图变化的规律:
6. 王鹏用小棒摆了四幅树状图,以下是树状图变化的规律:
王鹏按照这个规律继续往下摆,第五幅树状图要摆( )根小棒。
A、23 B、31 C、35 D、457. 下面每个图形都是由△、○、□中的两个(可以相同)构成的。观察各图形与它下面的数之间的关系,猜猜最右面图形下面的“?”表示( )。 A、23 B、31 C、13 D、328. 将正方形图①作如下操作:第1次,分别连接对边中点如图②,得到5个正方形(1个正方形加上4个中等正方形);第2次,将图②左上角正方形按上述方法再分割如图③,得到9个正方形;像这样操作8次,可以得到( )个正方形。
A、23 B、31 C、13 D、328. 将正方形图①作如下操作:第1次,分别连接对边中点如图②,得到5个正方形(1个正方形加上4个中等正方形);第2次,将图②左上角正方形按上述方法再分割如图③,得到9个正方形;像这样操作8次,可以得到( )个正方形。 A、29 B、32 C、33
A、29 B、32 C、33二、判断题
-
9.
 依次类推,摆5个三角形需要用小棒的根数是1+2×5=11(根)。( ) 10. 第⑤个点阵中点的个数是1+4×5=21(个)。( )
依次类推,摆5个三角形需要用小棒的根数是1+2×5=11(根)。( ) 10. 第⑤个点阵中点的个数是1+4×5=21(个)。( ) 11. 摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒.(判断对错)12. 操场的一边按3面红旗,4面黄旗,5面蓝旗插着一排彩旗.那么,第60面是蓝旗。( )13. ○▲□○▲□○▲□……,按照这样的规律摆,第20个图形是▲。( )
11. 摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒.(判断对错)12. 操场的一边按3面红旗,4面黄旗,5面蓝旗插着一排彩旗.那么,第60面是蓝旗。( )13. ○▲□○▲□○▲□……,按照这样的规律摆,第20个图形是▲。( )三、填空题
-
14. 1=12 ,
1+3=22 ,
1+3+5=32 ,
……
102=.
15. 找规律,写得数。
=1- , ,据上面等式,则:
16. 找规律,写结果。根据: , ,
那么: =
=
17. 有若干个棱长为1厘米的小正方体,如果把这些小正方体按如图所示的方式放置,当放置5层时,放置成的物体的表面积是平方厘米。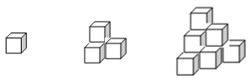 18. 自主探索。
18. 自主探索。
仔细观察上面的点子图,根据每个图中点子的排列规律,想一想,可以怎样计算每个图中点子的总个数?请你把下表填写完整。
序号
1
2
3
4
…
表示点子数的算式
1
1+4
…
点子的总个数
1
5
…
观察表中数据,如果用A表示第n个图形中点子的个数,A和n之间的关系可以表示成:
A= 。
19. 观察下图,每个图形中间是白色小正方形,周围是灰色小正方形。
照这样画下去,第10个图形中有个白色小正方形,个灰色小正方形。
20. 右图是一组有规律的图案,第1个图案是由4个基本图形组成,第2个图案是由7个基本图形组成,……则第5个图案是由个基本图形组成。
四、解答题
-
21. 下图中的数是“三角形数”。先观察图形,再完成练习。
 (1)、照样子画一画,并在括号里写出这个“三角形数”。(2)、第1个“三角形数”:1;第2个“三角形数”:1+2;第3个“三角形数”:1+2+3;……第n个“三角形数”:。22. 25是一个“正方形数”,下面表示25的不同构造方法中,分别可以用哪个算式表示?选一选,填一填。
(1)、照样子画一画,并在括号里写出这个“三角形数”。(2)、第1个“三角形数”:1;第2个“三角形数”:1+2;第3个“三角形数”:1+2+3;……第n个“三角形数”:。22. 25是一个“正方形数”,下面表示25的不同构造方法中,分别可以用哪个算式表示?选一选,填一填。
① 25 = 52
②25=1+3+5+7+9
③25=5+4+4+3+3+2+2+1+1
④25=1+2+3+4+5+4+3+2+1
23. 图①、②、③、④都是平面图形。 (1)、数一数每个图形各有多少个顶点,多少条边,这些边围出了多少个区城,将结果填入下表中(其中①已填好)。
(1)、数一数每个图形各有多少个顶点,多少条边,这些边围出了多少个区城,将结果填入下表中(其中①已填好)。图形
顶点数
边数
区域数
①
4
6
3
②
③
④
(2)、观察上表,推断一个平面图形的顶点数、边数、区域数之间的关系。(3)、现已知某一平面图形有999个顶点和999个区城,试根据(2)中推断出的关系,确定这个图形有多少条边。24. 将自然数1~100排列如下表:在这个表里用长方形框出的二行六个数(图中长方形框仅为示意),如果框起来的六个数的和为429,问这六个数中最小的数是几?(用方程解) 25. 如图,平面上分别有2个点,3个点,4个点,5个点……连一连,写出最多可以得到多少条线段。
25. 如图,平面上分别有2个点,3个点,4个点,5个点……连一连,写出最多可以得到多少条线段。
平面上点的数量与可以得到的线段的条数之间的关系:
26. 小华用边长是1厘米的小正方形摆出了下面的图形,并依次写出了每个图形的周长的算式,请你根据规律将表格填写完整。
正方形/个
1
4
9
( )
49
周长/厘米
4
4+6
4+6×2
4+6×3
( )
27. 挑战题如图叫“科克雪花”,它是瑞典科学家科克在1904年受雪花形状的启发而创造的。它的画法是这样的:
第一步,如图1,画出一个正三角形。
第二步,如图2,把这个正三角形的每条边三等分,以居中的一段为边向外作正三角形。
第三步,如图3,把居中的一段擦除。
如果继续上面的步骤,重复几次就得到了“科克雪花”。
 (1)、假如图1正三角形的边长为10厘米,那么图3的周长是厘米。(2)、假如图1正三角形的周长为n,请用含有n的代数式表示图4的周长。
(1)、假如图1正三角形的边长为10厘米,那么图3的周长是厘米。(2)、假如图1正三角形的周长为n,请用含有n的代数式表示图4的周长。