初中数学苏科版八年级上学期期末复习专题（3） 轴对称图形及轴对称的性质
试卷更新日期：2020-12-14 类型：复习试卷
一、单选题
-
1. 下列图案中，有且只有三条对称轴的是（ ）A、
B、
C、
D、
2. 如图， ABC和 关于直线L对称，下列结论：① ABC≌ ；②∠BAC＝ ；③直线L垂直平分 ；④直线L平分 .正确的有（ ）
A、4个 B、3个 C、2个 D、1个3. 如图是一个经过改造的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出（球可以经过多次反射），那么该球最后将落入的球袋是（ ）
A、1号袋 B、2号袋 C、3号袋 D、4号袋4. 娜娜跟奶奶学习剪纸艺术，想把一张正方形纸片从中间剪出一个如图 的形状.现在将正方形纸片按如图所示的步骤①，②沿虚线对折两次，然后沿虚线剪去一个角，展开铺平，娜娜的剪裁方法应该是（ ）
A、
B、
C、
D、
5. 如图，将长方形 纸片沿对角线 折叠，使点 落在 处， 交AD于E，若 ，则在不添加任何辅助线的情况下，则图中 的角（虚线也视为角的边）的个数是（ ）
A、5个 B、4个 C、3个 D、26. 如图，在 中， ，将 沿直线 翻折，点 落在点 的位置，则 的度数是（ ）
A、 B、 C、 D、7. 如图，在△ABC中，点D、E在BC边上，点F在AC边上，将△ABD沿着AD翻折，使点B和点E重合，将△CEF沿着EF翻折，点C恰与点A重合．结论：①∠BAC=90°，②DE=EF，③∠B=2∠C，④AB=EC，正确的有（ ）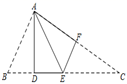
A、①②③④ B、③④ C、①②④ D、①②③8. 如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，则∠1+∠2的度数为（ ）
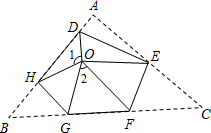A、120° B、135° C、150° D、180°9. 如图，△ABE，△ADC是△ABC分别沿着边AB，AC翻折形成的，若∠BCA：∠ABC：∠BAC=28：5：3，BE与DC交于点F，则∠BFC的度数为（ ）
A、15° B、20° C、30° D、36°10. 如图，分别以△ABC的边AB，AC所在直线为对称轴作△ABC的对称图形△ABD和△ACE，∠BAC＝150°，线段BD与CE相交于点O，连接BE、ED、DC、OA.有如下结论：①∠EAD＝90°；②∠BOE＝60°；③OA平分∠BOC；④ED＝2EA；⑤BP＝EQ.其中正确的结论个数是（ ）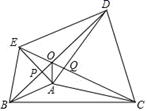
A、2 B、3 C、4 D、5二、填空题
-
11. 小明从镜子里看到镜子对面电子钟的像如图所示，则实际时间是 ．
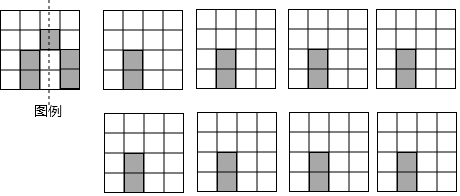
12. 如图，在正方形网格中有两个小正方形被涂黑，再涂黑一个图中其余的小正方形，使得整个被涂黑的图案构成一个轴对称图形，那么涂法共有种.
13. 如图，把一张长方形纸片 沿 折叠后，点 落在 边上的 处，点 落在 处，若 ，则图中 度数等于.
14. 如图，∠MON内有一点P，P点关于OM的轴对称点是G，P点关于ON的轴对称点是H，GH分别交OM、ON于A、B点，若∠MON=35°，则∠GOH=.
15. 如图， 和 分别是关于AB，AC边所在直线的轴对称图形，若∠1：∠2：∠3＝7：2：1，则∠α的度数为.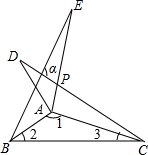
16. 如图，在 的正方形格纸中，有一个以格点为顶点的 ，在格纸中能画出与 成轴对称且也以格点为顶点的三角形（不包括 本身），这样的三角形共有个.
17. 如图1是长方形纸带， ∠DEF=17°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中的∠CFE的度数是.
18. 如图，将△ABC沿着过AB中点D的直线折叠，使点A落在BC边上的A1 ， 称为第1次操作，折痕DE到BC的距离记为h1；还原纸片后，再将△ADE沿着过AD中点D1的直线折叠，使点A落在DE边上的A2处，称为第2次操作，折痕D1E1到BC的距离记为h2：按上述方法不断操作下去…，经过第2019次操作后得到的折痕D2018E2018 ， 到BC的距离记为h2019：若h1＝1，则h2019的值为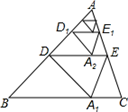
三、解答题
-
19. 如图，是由4×4个大小完在一样的小正方形组成的方格纸，其中有两个小正方形是涂黑的，请再选择三个小正方形并涂黑，使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
20. 画图并回答问题：如图所示，在边长为 的正方形网格中，有一格点三角形 （三角形的三个顶点都在小正方形的顶点上）．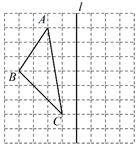
(1)、请画出 关于直线 的对称的 ；(2)、 的面积是 ．21. 如图，△ABC中，∠A＝90°，D为AC上一点，E为BC上一点，点A和点E关于BD对称，点B和点C关于DE对称.求∠ABC和∠C的度数.
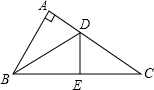22. 长方形纸片OABC中，AB=10cm，BC=6cm，把这张长方形纸片OABC如图放置在平面直角坐标系中，在边OA上取一点E，将△ABE沿BE折叠，使点A恰好落在OC边上的点F处．
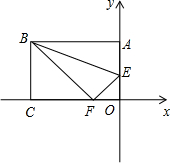(1)、求点E、F的坐标；(2)、在AB上找一点P，使PE+PF最小，求点P坐标；(3)、在（2）的条件下，点Q（x，y）是直线PF上一个动点，设△OCQ的面积为S，求S与x的函数关系式．23. 如图
(1)、如图（1），把三角形纸片ABC的角A沿DE折起（DE为折痕），使顶点A在∠A的内部，点A的对称点为点O，判断∠O、∠ODC、∠BEO的大小关系，并写出证明过程．(2)、如图（2），把三角形纸片ABC的角A沿DE折起（DE为折痕），使顶点A在∠A的外部，点A的对称点为点O，判断∠O、∠ODC、∠BEO的大小关系吗？并写出证明过程．24. 如图①所示，在三角形纸片 中， ， ，将纸片的一角折叠，使点 落在 内的点 处.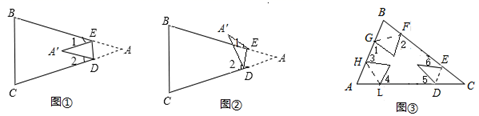
(1)、若 ， .(2)、如图①，若各个角度不确定，试猜想 ， ， 之间的数量关系，直接写出结论.②当点 落在四边形 外部时（如图②），（1）中的猜想是否仍然成立？若成立，请说明理由，若不成立， ， ， 之间又存在什么关系？请说明.
(3)、应用：如图③：把一个三角形的三个角向内折叠之后，且三个顶点不重合，那么图中的 和是.25. （问题探究）将三角形 纸片沿 折叠，使点A落在点 处.
(1)、如图，当点A落在四边形 的边 上时，直接写出 与 之间的数量关系；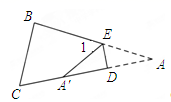
(2)、如图，当点A落在四边形 的内部时，求证： ；
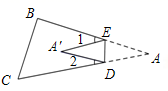(3)、如图，当点A落在四边形 的外部时，探索 ， ， 之间的数量关系，并加以证明；
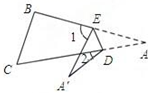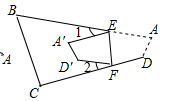
(4)、（拓展延伸）如图，若把四边形 纸片沿 折叠，使点A、D落在四边形 的内部点 、 的位置，请你探索此时 ， ， ， 之间的数量关系，写出你发现的结论，并说明理由.
26. 阅读理解如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重复部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．
小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．
探究发现
(1)、△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？（填“是”或“不是”）．(2)、小丽经过三次折叠发现了∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．
(3)、应用提升小丽找到一个三角形，三个角分别为15°、60°、105°，发现60°和105°的两个角都是此三角形的好角．
请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．