初中数学苏科版八年级上学期期末复习专题(2) 探索三角形全等的条件
试卷更新日期:2020-12-14 类型:复习试卷
一、单选题
-
1. 能判定 与 全等的条件是( )A、 , , B、 , , C、 , , D、 , ,2. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )A、
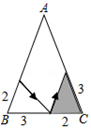 B、
B、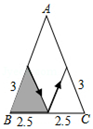 C、
C、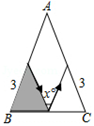 D、
D、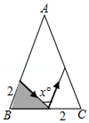 3. 在如图所示的 6×6 网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数( )
3. 在如图所示的 6×6 网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数( )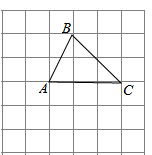 A、3 个 B、4 个 C、6 个 D、7 个4. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )
A、3 个 B、4 个 C、6 个 D、7 个4. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )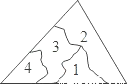 A、1;SAS B、2;ASA C、3;ASA D、4;SAS5. △ABC中,AC=5,中线AD=7,则AB边的取值范围是( )A、9<AB<19 B、5<AB<19 C、4<AB<12 D、2<AB<126. 如图, , , ,下列条件中不能判断 的是( )
A、1;SAS B、2;ASA C、3;ASA D、4;SAS5. △ABC中,AC=5,中线AD=7,则AB边的取值范围是( )A、9<AB<19 B、5<AB<19 C、4<AB<12 D、2<AB<126. 如图, , , ,下列条件中不能判断 的是( ) A、 B、 C、 D、7. 如图,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:其中正确的结论有( )
A、 B、 C、 D、7. 如图,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:其中正确的结论有( )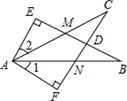
①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN;⑤△AFN≌△AEM.
A、2个 B、3个 C、4个 D、5个8. 如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F , AD交CE于G . 则下列结论中错误的是( ) A、AD=BE B、BE⊥AC C、△CFG为等边三角形 D、FG∥BC9. △ABC 中,AB=AC=12 厘米,∠B=∠C,BC=8 厘米,点 D 为 AB 的中点.如果点 P 在线段 BC 上以 2 厘米/秒 的速度由 B 点向 C 点运动,同时,点 Q 在线段 CA 上由 C 点向 A 点运动.若点 Q 的运动速度为 v 厘米/秒,则当△BPD 与△CQP 全等时,v 的值为( )
A、AD=BE B、BE⊥AC C、△CFG为等边三角形 D、FG∥BC9. △ABC 中,AB=AC=12 厘米,∠B=∠C,BC=8 厘米,点 D 为 AB 的中点.如果点 P 在线段 BC 上以 2 厘米/秒 的速度由 B 点向 C 点运动,同时,点 Q 在线段 CA 上由 C 点向 A 点运动.若点 Q 的运动速度为 v 厘米/秒,则当△BPD 与△CQP 全等时,v 的值为( ) A、2 B、5 C、1 或 5 D、2 或 310. 如图,等腰 中, , 于 . 的平分线分别交 , 于点 , 两点, 为 的中点,延长 交 于点 ,连接 .下列结论:① ;② ;③ 是等腰三角形;④ .其中正确的结论个数是( )
A、2 B、5 C、1 或 5 D、2 或 310. 如图,等腰 中, , 于 . 的平分线分别交 , 于点 , 两点, 为 的中点,延长 交 于点 ,连接 .下列结论:① ;② ;③ 是等腰三角形;④ .其中正确的结论个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在平面直角坐标系中,已知点A,B的坐标分别是 , ,若在x轴下方有一点P,使以O,A,P为顶点的三角形与 全等,则满足条件的P点的坐标是 .12. 如图所示, , , ,若 则
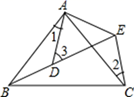 13. 如图,已知△ABC 为等边三角形,点 D、E 分别在边 BC、AC 上,且 AE=CD,AD 与 BE相交于点 F.则∠DFE 的度数为°;
13. 如图,已知△ABC 为等边三角形,点 D、E 分别在边 BC、AC 上,且 AE=CD,AD 与 BE相交于点 F.则∠DFE 的度数为°; 14. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=
14. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=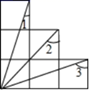 15. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为秒时,△ABP和△DCE全等.
15. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为秒时,△ABP和△DCE全等. 16. 如图, 的面积为 , 平分 , 于 ,则 的面积为;
16. 如图, 的面积为 , 平分 , 于 ,则 的面积为; 17. 如图,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF= ∠BAD,延长FD到点G,使DG=BE,连接AG,下列结论:①△ABE≌△ADG;②△AEF≌△AGF;③EF=BE+DF;④AD+BE>AF,正确的有
17. 如图,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF= ∠BAD,延长FD到点G,使DG=BE,连接AG,下列结论:①△ABE≌△ADG;②△AEF≌△AGF;③EF=BE+DF;④AD+BE>AF,正确的有 18. 如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD、CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD、CD、BE、CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接CD、BE、CE、BF、CF;…,依次规律,第200个图形中有全等三角形的对数是.
18. 如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD、CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD、CD、BE、CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接CD、BE、CE、BF、CF;…,依次规律,第200个图形中有全等三角形的对数是.
三、综合题
-
19. 在△ABC中,AB⊥BC , AB = BC , E为BC上一点,连接AE , 过点C作CF⊥AE , 交AE的延长线于点F , 连结BF , 过点B作BG⊥BF交AE于G .
 (1)、求证:△ABG ≌ △CBF;(2)、若E为BC中点,求证:CF + EF = EG.20. 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,亚足分别为D、E。
(1)、求证:△ABG ≌ △CBF;(2)、若E为BC中点,求证:CF + EF = EG.20. 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,亚足分别为D、E。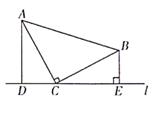 (1)、求证:△ADC≌△CEB.(2)、请判断DE、BE、AD三条线段之间有怎样的数基关系,并证明。21. 已知:如图,AF平分∠BAC , BC⊥AF , 垂足为E , CD∥AB交AF于点D , PB分别与线段CF , AF交于点P , M .
(1)、求证:△ADC≌△CEB.(2)、请判断DE、BE、AD三条线段之间有怎样的数基关系,并证明。21. 已知:如图,AF平分∠BAC , BC⊥AF , 垂足为E , CD∥AB交AF于点D , PB分别与线段CF , AF交于点P , M . (1)、求证:AB=CD;(2)、若∠BAC=2∠MPC , 请你判断∠F与∠MCD的数量关系,并说明理由.22. 已知:在 中, , 为过点 的一条直线,分别过 两点作 ,垂足分别为 .
(1)、求证:AB=CD;(2)、若∠BAC=2∠MPC , 请你判断∠F与∠MCD的数量关系,并说明理由.22. 已知:在 中, , 为过点 的一条直线,分别过 两点作 ,垂足分别为 .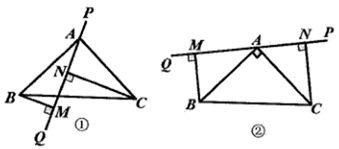 (1)、如图①所示,当 与 边有交点时,求证: ;(2)、如图②所示,当 与 边不相交时,请写出线段 和 之间的数量关系,并说明理由.23. 在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE。
(1)、如图①所示,当 与 边有交点时,求证: ;(2)、如图②所示,当 与 边不相交时,请写出线段 和 之间的数量关系,并说明理由.23. 在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE。 (1)、如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE=。(2)、设∠BAC=α,∠BCE=β
(1)、如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE=。(2)、设∠BAC=α,∠BCE=β①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由。
②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出结论。
24. 如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5 cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点Р运动结束时,点О运动随之结束).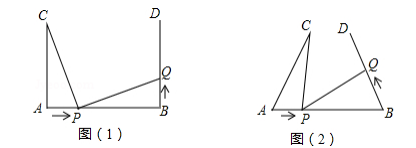 (1)、若点Q的运动速度与点Р的运动速度相等,当t =1s时,△ACP与△BPO是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)、如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,点O的运动速度为x cm/s ,其它条件不变,当点P、O运动到何处时有△ACP与△BPO全等,求出相应的x的值.25. 如图
(1)、若点Q的运动速度与点Р的运动速度相等,当t =1s时,△ACP与△BPO是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)、如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,点O的运动速度为x cm/s ,其它条件不变,当点P、O运动到何处时有△ACP与△BPO全等,求出相应的x的值.25. 如图 (1)、如图①,在△ABC中,∠BAC=90∘,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D. E证明:DE=BD+CE.(2)、如图②,将(1)中的条件改为:在△ABC中,AB=AC,D.A. E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请问结论DE=BD+CE是否成立,若成立,请你给证明:若不存在,请说明理由。(3)、应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,D.A. E三点都在直线m上,且∠BDA=∠AEC=∠BAC,只出现m与BC的延长线交于点F,若BD=5,DE=7,EF=2CE,求△ABD与△ABF的面积之比。26. 已知△ABC 是等腰直角三角形, BC = AC ,∠ABC = ∠BAC ,直角顶点 C 在 x 轴上,一锐角顶点 B 在 y 轴上.
(1)、如图①,在△ABC中,∠BAC=90∘,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D. E证明:DE=BD+CE.(2)、如图②,将(1)中的条件改为:在△ABC中,AB=AC,D.A. E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请问结论DE=BD+CE是否成立,若成立,请你给证明:若不存在,请说明理由。(3)、应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,D.A. E三点都在直线m上,且∠BDA=∠AEC=∠BAC,只出现m与BC的延长线交于点F,若BD=5,DE=7,EF=2CE,求△ABD与△ABF的面积之比。26. 已知△ABC 是等腰直角三角形, BC = AC ,∠ABC = ∠BAC ,直角顶点 C 在 x 轴上,一锐角顶点 B 在 y 轴上. (1)、如图①若 AD 于垂直 x 轴,垂足为点 D .点 C 坐标是( -1, 0) ,点 A 的坐标是( -3,1) , 求点 B 的坐标.(2)、如图②,直角边 BC 在两坐标轴上滑动,若 y 轴恰好平分 ∠ABC , AC 与 y 轴交于点D ,过点 A 作 AE⊥y 轴于 E ,请猜想 BD 与 AE 有怎样的数量关系,并证明你的猜想.(3)、如图③,直角边 BC 在两坐标轴上滑动,使点 A 在第四象限内,过 A 点作 AF⊥ y 轴于 F ,在滑动的过程中,两个结论① 为定值;② 为定值,只有一个结论成立,请你判断正确的结论加并求出定值.
(1)、如图①若 AD 于垂直 x 轴,垂足为点 D .点 C 坐标是( -1, 0) ,点 A 的坐标是( -3,1) , 求点 B 的坐标.(2)、如图②,直角边 BC 在两坐标轴上滑动,若 y 轴恰好平分 ∠ABC , AC 与 y 轴交于点D ,过点 A 作 AE⊥y 轴于 E ,请猜想 BD 与 AE 有怎样的数量关系,并证明你的猜想.(3)、如图③,直角边 BC 在两坐标轴上滑动,使点 A 在第四象限内,过 A 点作 AF⊥ y 轴于 F ,在滑动的过程中,两个结论① 为定值;② 为定值,只有一个结论成立,请你判断正确的结论加并求出定值.