初中数学苏科版八年级上学期期末复习专题（1） 全等图形及全等三角形的性质
试卷更新日期：2020-12-14 类型：复习试卷
一、单选题
-
1. 有下面的说法：①全等三角形的形状相同；②全等三角形的对应边相等；③全等三角形的对应角相等；④全等三角形的周长、面积分别相等．其中正确的说法有（ ）A、1个 B、2个 C、3个 D、4个2. 如图，△ABC≌△ADE，∠DAC=70°，∠BAE=100°，BC、DE相交于点F，则∠DFB度数是（ ）
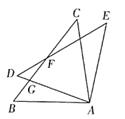A、15° B、20° C、25° D、30°3. 如图，点D、E在△ABC的边BC上，△ABD≌△ACE，下列结论不一定成立的是（ ）
A、 B、 C、 D、4. 如图，已知AB=CD且AB⊥CD，连接AD，分别过点C，B作CE⊥AD，BF⊥AD，垂足分别为E，F.若AD=10，CE=8，BF=6，则EF的长为（ ）
A、4 B、3.5 C、3 D、2.55. 如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE.下列说法：①CE＝BF；②△ABD和△ACD的面积相等；③BF∥CE；④△BDF≌△CDE.其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个6. 如图，在4x4的正方形网格中，∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数为（ ）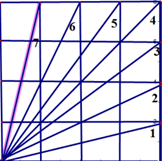
A、300° B、315° C、320° D、325°7. 已知：如图，在长方形ABCD中，AB=4，AD=6.延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC-CD-DA向终点A运动，设点P的运动时间为 秒，当 的值为_____秒时，△ABP和△DCE全等.
A、1 B、1或3 C、1或7 D、3或78. 如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE，下列说法：①△ABD 和△ACD面积相等；②∠BAD＝∠CAD；③△BDF≌△CDE；④BF∥CE；⑤CE＝AE，其中正确的是（ ）
A、①② B、③⑤ C、①③④ D、①④⑤9. 如图所示，△ABC≌△ADE，AB=AD，AC=AE，BC的延长线交DA于点F，交DE于点G，∠AED=105°，∠CAD=15°，∠B=30°，则∠1的度数为（ ）．
A、50° B、60° C、40° D、20°10. 如图，锐角△ABC中，D、E分别是AB、AC边上的点，△ADC≌△ADC′，△AEB≌△AEB′，且C′D∥EB′∥BC，BE、CD交于点F．若∠BAC=35°，则∠BFC的大小是（ ）
A、105° B、110° C、100° D、120°二、填空题
-
11. 如图，△ABC≌△ADE，若∠BAE=120°，∠BAD=40°，则∠BAC=°
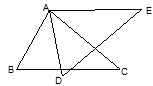12. 三个全等三角形按如图的形式摆放，则 度.
13. 一个三角形的三边为2、5、x+2y，另一个三角形的三边为2x+y、2、4，若这两个三角形全等，则x+y＝.14. 如图，
中，∠ 
900 ， ∠A＝200 ， △ABC≌△ ，若 恰好经过点B， 交AB于D，则 
的度数为 °． 
15. 如图所示的网格是正方形网格，图形的各个顶点均为格点，则∠1+∠2=.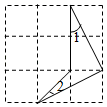
16. 如图，CA⊥AB，垂足为点A，AB=8厘米，AC=4厘米，射线BM⊥AB，垂足为点B，一动点E从A点出发以2厘米/秒的速度沿射线AN运动，点D为射线BM上一动点，随着E点运动而运动，且始终保持ED=CB，当点E离开点A后，运动 秒时，△DEB与△BCA全等.
17. 如图，在△ABC中，AB＝AC＝24厘米，∠B=∠C ，BC＝16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为厘米/秒时，能够在某一时刻使△BPD与△CQP全等．
18. 如图，直线 经过 的直角顶点 的边上有两个动点 ，点 以 的速度从点 出发沿 移动到点 ，点 以 的速度从点 出发，沿 移动到点 ，两动点中有一个点到达终点后另一个点继续移动到终点过点 分别作 ，垂足分别为点 .若 ，设运动时间为 ，则当 时，以点 为顶点的三角形与以点 为顶点的三角形全等.
三、综合题
-
19. 如图，已知△ACF≌△DBE，且点A、B、C、D在同一条直线上，
∠A=40°，∠F=50°
(1)、求△DBE各内角度数(2)、若AD=16，BC=10，求AB的长.20.(1)、如图， ，且 ， ， ，求 的度数.
(2)、已知a，b，c为 的三边长，化简： .21. 如图，AC平分∠BAD，CE⊥AB，CD⊥AD，点E、D为垂足，CF＝CB．
(1)、求证：BE＝FD；(2)、若AC＝10，AD＝8，求四边形ABCF的面积．22. 如图，在△ABC中，BD⊥AC ， 垂足为C ， 且∠A＜∠C ， 点E是一动点，其在BC上移动，连接DE ， 并过点E作EF⊥DE ， 点F在AB的延长线上，连接DF交BC于点G ．
(1)、请同学们根据以上提示，在上图基础上补全示意图．(2)、当△ABD与△FDE全等，且AD＝FE ， ∠A＝30°，∠AFD＝40°，求∠C的度数．23. 如图①， 、 分别为线段 上的两个动点，且 于 ， 于 ，若 ， ， 交 于点 .
(1)、求证： ， ；(2)、当 ， 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由.24.通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连结EF，试猜想EF、BE、DF之间的数量关系．
(1)、思路梳理把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，由∠ADG=∠B=90°，得∠FDG=180°，即点F、D、G共线，易证△AFG≌ ， 故EF、BE、DF之间的数量关系
为 ．
(2)、类比引申如图2，点E、F分别在正方形ABCD的边CB、DC的延长线上，∠EAF=45°，连结EF，试猜想EF、BE、DF之间的数量关系为 ， 并给出证明．
(3)、联想拓展如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠BAD+∠EAC=45°，若BD=3，EC=6，求DE的长．
25.
(1)、问题背景：如图 1，在四边形 ABCD 中，AB = AD，∠BAD= 120°，∠B =∠ADC= 90°，E，F 分别是 BC， CD 上的点，且∠EAF = 60°，探究图中线段BE，EF，FD之间的数量关系.
小明同学探究此问题的方法是延长FD到点G，使DG=BE， 连结AG，先证明Δ ΔADG，再证明Δ ΔAGF，可得出结论，他的结论应是.
(2)、探索延伸：如图 2，在四边形ABCD 中，AB=AD，∠B+∠D=180°，E，F分别是BC，CD上的点，∠EAF= ∠BAD，上述结论是否依然成立？并说明理由.
26.
(1)、问题背景：如图1，在四边形 中， ， ， ， ， ， 绕B点旋转，它的两边分别交 、 于E、F.探究图中线段 ， ， 之间的数量关系.小李同学探究此问题的方法是：延长 到G，使 ，连接 ，先证明 ，再证明 ，可得出结论，他的结论就是；(2)、探究延伸1：如图2，在四边形 中， ， ， ， ， 绕B点旋转，它的两边分别交 、 于E、F.上述结论是否仍然成立？请直接写出结论（直接写出“成立”或者“不成立”），不要说明理由.(3)、探究延伸2：如图3，在四边形 中， ， ， ， 绕B点旋转，它的两边分别交 、 于E、F.上述结论是否仍然成立？并说明理由.(4)、实际应用：如图4，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西 的A处舰艇乙在指挥中心南偏东 的B处，并且两舰艇到指挥中心的距离相等接到行动指令后，舰艇甲向正东方向以75海里/小时的速度前进，同时舰艇乙沿北偏东 的方向以100海里/小时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达E、F处，且指挥中心观测两舰艇视线之间的夹角为 ，试求此时两舰艇之间的距离.