浙江省温岭市团队六校2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2020-12-14 类型：期中考试

进入出卷网下载

一、单选题

1. 如果收入10元记作 $+ 10$ 元，那么支出10元记作（）

A、 $+ 10$ 元 B、 $- 10$ 元 C、 $+ 20$ 元 D、 $- 20$ 元

查看试题解析
2. 下列各数中，比 $- 2$ 大的数是（）

A、 $- 3$ B、 $- \frac{9}{2}$ C、0 D、 $- 2$

查看试题解析
3. 如图，O为原点，数轴上A ， B ， O ， C四点，表示的数与点A所表示的数是互为相反数的点是（）

A、点B B、点O C、点A D、点C

查看试题解析
4. 单项式-5ab³的系数是（　　　）

A、5 B、-5 C、4 D、3

查看试题解析
5. 下列计算正确的是（）

A、 $2 x - x = 2$ B、 $a b^{2} + 3 b a^{2} = 4 a b^{2}$ C、 $x^{2} y z - 2 x^{2} y z = - x^{2} y z$ D、 $m^{2} + 5 n = 6 m^{2} n$

查看试题解析
6. 下列计算正确的是（　　　）

A、 $(- \frac{7}{8}) \times 15 \times (- 1 \frac{1}{7}) = - (\frac{7}{8} \times \frac{8}{7}) \times 15 = - 15$ B、 $12 \times (\frac{1}{3} - \frac{1}{4} - 1) = 4 - 3 - 1 = 0$ C、 $(- 9) \times 5 \times (- 4) \times 0 = 9 \times 5 \times 4 = 180$ D、 $(- 5) \times (- 4) \times (- 2) \times (- 2) = 5 \times 4 \times 2 \times 2 = 80$

查看试题解析
7. 下列代数式中，去括号后结果等于a﹣b﹣c的是（　　　）

A、﹣（a+b+c） B、﹣c+（b﹣a） C、a﹣（b﹣c） D、﹣b﹣（c﹣a）

查看试题解析
8. 若 $| b + 2 | + {(a - 3)}^{2} = 0$ ，则 $b^{a}$ 的值为（　　　）

A、﹣b B、 $- \frac{1}{8}$ C、﹣8 D、8

查看试题解析
9. 1261年，我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律，我们把这个三角形称为“杨辉三角”，请观察图中的数字排列规律，则代数式a+b+c的值为（）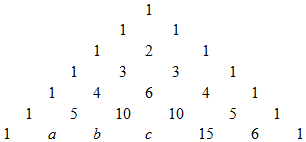

A、22 B、41 C、50 D、51

查看试题解析
10. 近几年来，在欧美等国家流行一种“数独”推理游戏，游戏规则如下：①9×9的九宫格子中，分成9个3×3的小九宫格，用1，2，3，…，9这9个数字填满整个格子，且每个格子只能填一个数；②每一行与每一列以及每个小九宫格里分别都有1，2，3，…9的所有数字.根据图中已填入的数字，可以判断A处填入的数字是（　　　）

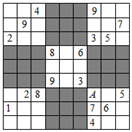A、9 B、8 C、2 D、1

查看试题解析

二、填空题

11. 2020的倒数是。

查看试题解析
12. 用“＞”或“＜”填空：|﹣1|0.

查看试题解析
13. 某种零件的直径规格是20±0.2mm，经检查，一个零件的直径18 mm，该零件（填“合格”或“不合格”）；

查看试题解析
14. 据相关报道，开展精准扶贫工作五年以来，我国约有56000000人摆脱贫困，将56000000用科学记数法表示是.

查看试题解析
15. 减去 $3 m$ 后，等于 $3 m^{2} + m - 1$ 的多项式是.

查看试题解析
16. 11.49精确到个位的近似值为.

查看试题解析
17. 若单项式 $2 x^{m - 1} y^{2}$ 与单项式 $\frac{1}{3} x^{2} y^{n + 1}$ 是同类项，则 $m + n =$ .

查看试题解析
18. 如果代数式 $- 2 a + 3 b + 5$ 的值为 $15$ ，那么 $- 6 a + 9 b + 2 =$ .

查看试题解析
19. 扑克牌游戏中，将一些扑克牌分成左、中、右相同的三份.小明背对小亮，让小亮按下列三个步骤操作：第一步：从左边取3张扑克牌，放在中间，右边不变；
第二步：从右边取2张扑克牌，放在中间，左边不变；

第三步：从中间取与左边相同张数的扑克牌，放在左边，右边不变.

这时，小明准确说出了中间一堆牌现有的张数，你认为中间一堆的张数是.

查看试题解析
20. 如图，连接在一起的两个正方形的边长都为1cm，现有一个微型机器人由点A开始按从A→B→C→D→E→F→C→G→A…的顺序沿正方形的边循环移动.当微型机器人移动了2020cm时，它停在点.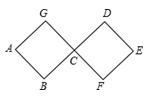

查看试题解析

三、解答题

21. 计算：

(1)、-7+8-（-2）

(2)、 $3 \div 4 \times (- \frac{1}{4})$

(3)、 $- (- 8) \div 4 + (- \frac{1}{2} + \frac{3}{4}) \times (- 8)$

(4)、 $- 1^{2020} - \frac{1}{3} \times [(- 5) \times {(- \frac{3}{5})}^{2} + 0.8]$

查看试题解析
22. 先化简，再求值： $- 3 x^{2} + 5 x + 0.5 x^{2} - x + 1,$ 其中x=-1.

查看试题解析
23. 某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下（规定向南为正，向北为负，单位：km）：

第1批

第2批

第3批

第4批

第5批

5km

2km

﹣4km

﹣3km

10km

(1)、接送完第5批客人后，该驾驶员在公司什么方向，距离公司多少千米？

(2)、若该出租车每千米耗油0.2升，那么在这过程中共耗油多少升？

(3)、若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？

查看试题解析
24. 规定运算△为：若a＞b，则a△b=a+b；若a＜b，则a△b=a×b；若a=b，则a△b=a﹣b+1.

(1)、计算6△（-4）的值；

(2)、计算（（-2）△3）+（4△4）+（7△5）的值.

查看试题解析
25. 如图1，A纸片是边长为a的正方形，B纸片是边长为b的正方形，C纸片是长为b，宽为a的长方形.现用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形.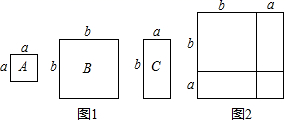

(1)、请用两种不同的方法求图2大正方形的面积.
方法1：；方法2：；

(2)、观察图2，请你写出下列三个代数式：（a+b）² ， a²+b² ， ab之间的等量关系；

(3)、根据（2）题中的等量关系，解决如下问题：若a+b=5，a²+b²=13，求ab的值；

查看试题解析
26. “收获是努力得来的”，在数轴上，若点C到点A的距离刚好是3，则点C叫做点A的“收获点”，若点C到A、B两点的距离之和为6，则点C叫做A、B的“收获中心”.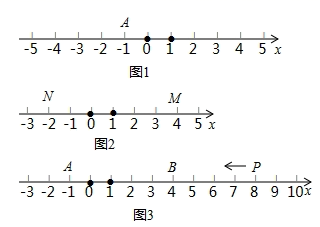

(1)、如图1，点A表示的数为﹣1，则A的收获点C所表示的数应该是；

(2)、如图2，M、N为数轴上两点，点M所表示的数为4，点N所表示的数为﹣2，点C就是M、N的收获中心，则C所表示的数可以是（填一个即可）；

(3)、如图3，A、B、P为数轴上三点，点A所表示的数为﹣1，点B所表示的数为4，点P所表示的数为8，现有一只电子蚂蚁从点P出发，以2个单位每秒的速度向左运动，当经过t秒时，电子蚂蚁是A和B的收获中心，求t的值.

查看试题解析

第1批	第2批	第3批	第4批	第5批
5km	2km	﹣4km	﹣3km	10km