浙江省绍兴市新昌县2020-2021学年七年级上学期数学期中考试试卷
试卷更新日期:2020-12-14 类型:期中考试
一、单选题
-
1. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为( )A、 B、 C、 D、2. 一种巧克力的质量标识为“25±0.25千克”,则下列哪种巧克力是合格的( )A、25.30千克 B、24.70千克 C、25.51千克 D、24.80千克3. - 2的相反数是( )A、- B、-2 C、 D、24. (-2)5表示( )A、5乘以(-2)的积 B、5个(-2)连乘的积 C、2个-5相乘的积 D、5个(-2)相加的和5. 下列运算正确的是( )A、 =±3 B、(﹣2)3=8 C、﹣22=﹣4 D、﹣|﹣3|=36. 在一个峡谷中,测得A地的海拔为﹣11m,B地比A地高15m,C地比B地低7m,则C地的海拔为( )A、11 B、﹣19 C、3 D、﹣37. 估计 的大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间8. 若有理数m在数轴上对应的点为M,且满足 ,则下列数轴表示正确的是 ( )A、
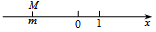 B、
B、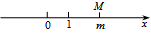 C、
C、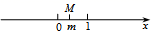 D、
D、 9. 有下列说法:
9. 有下列说法:①任何无理数都是无限小数;②有理数与数轴上的点一一对应;③在数轴上,原点两旁的两个点所表示的数都是互为相反数;④ 是分数,它是有理数; ⑤ 的算术平方根是9. 其中正确的个数是( )
A、1 B、2 C、3 D、410. 若 ,则我们把 称为 的“哈利数”,如3的“哈利数”是 ,-2的“哈利数”是 ,已知 , 是 的“哈利数”, 是 的“哈利数”, 是 的“哈利数”,……,依此类推,则 =( )A、3 B、-2 C、 D、二、填空题
-
11. 如果收入100元记作+100元,那么支出50元记作元.
12. 由四舍五入法得到的近似数7.530万,精确到位.13. ﹣ 的倒数是 .14. 若|a|=5,b=﹣2,且ab>0,则a+b= .15. 若x,y为实数,且|x﹣2|+ =0,则(x+y)2020的值为.16. 若 是m的一个平方根,则m+22的算术平方根是.17. 比较大小:2 3 ; .18. 已知有理数 满足 ,则 的值为 .19. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满五进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是.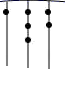
三、解答题
-
20. 把下列各数填在相应的表示集合的大括号内:
﹣2,π,﹣ ,﹣|﹣3|, ,﹣0.3,﹣ ,1.7, ,0,1.1010010001…(每两个1之间依次多一个0),
整数{ …} 负分数{ …} 无理数{ …}.
21. 如图,根据给出的数轴,解答下列问题: (1)、A,B两点之间的距离是;(2)、数轴上,线段AB的中点表示的数是.(3)、画出与点A距离为2的点.(用不同于A,B的字母在所给的数轴上表示)22.(1)、(2)、(﹣5)÷5×(3)、(4)、(﹣1)2020+ +(﹣3)﹣4223. 某一出租车一天下午以鼓楼为出发点,在东西方向上营运,向东为正,向西为负,行车依先后次序记录如下:(单位:km)
(1)、A,B两点之间的距离是;(2)、数轴上,线段AB的中点表示的数是.(3)、画出与点A距离为2的点.(用不同于A,B的字母在所给的数轴上表示)22.(1)、(2)、(﹣5)÷5×(3)、(4)、(﹣1)2020+ +(﹣3)﹣4223. 某一出租车一天下午以鼓楼为出发点,在东西方向上营运,向东为正,向西为负,行车依先后次序记录如下:(单位:km)+9,-3,-5,+4,-8,+6,-3,-6,-4,+7,+4
(1)、将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼什么方向?(2)、若每千米的价格为3元,司机一下午的营业额是多少元?
