四川省德阳市广汉市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-14 类型:期中考试
一、单选题
-
1. 有下列现象:①地下水位逐年下降:②传送带的移动;③方向盘的转动:④水龙头开关的转动;⑤钟摆的运动:⑥荡秋千运动。其中属于旋转的有( )A、2个 B、3个 C、4个 D、5个2. 一元二次方程x2+x﹣2=0根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定3. 若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为( )A、 B、 C、 D、4. 已知关于 的一元二次方程 ,若此方程的一个根是1,则方程的另一个根( )A、1 B、2 C、3 D、4.5. 关于y=2(x﹣3)2+2的图象,下列叙述正确的是( )A、顶点坐标为(﹣3,2) B、对称轴为直线y=3 C、当x≥3时,y随x增大而增大 D、当x≥3时,y随x增大而减小6. 某初中毕业班的每一个同学都将自己的相片向全班其他同学各送一张表示留念,全班共送了2550张相片,如果全班有x名学生,根据题意,列出方程为( )
A、 B、 C、 D、7. 设A(-1, )、B(1, )、C(3, )是抛物线 上的三个点,则 、 、 的大小关系是( )A、 < < B、 < < C、 < < D、 < <8. 已知 的两根分别是 和 则 的值是( )A、2 B、-2 C、 D、9. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、10. 二次函数与 的图象与 轴有交点,则 的取值范围是( )A、 B、 C、 且 D、 且11. 三角形两边长分别为2和4,第三边是方程x2-6x+8=0的解,则这个三角形的周长是( ).A、8 B、8或10 C、10 D、8和1012. 如图,二次函数 (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是( )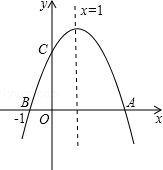 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
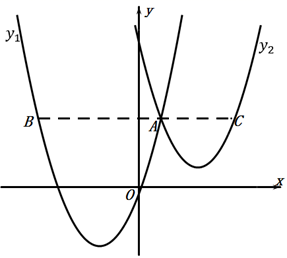
13. 观察:① ;② ;③ ;④ ;⑤ ;⑥ .这六个式子中二次函数有 . (只填序号)14. 方程x2=2x的解是.15. 将二次函数 化成 的形式为.16. 函数y=x2+bx-c的图象经过点(1,2),则b-c的值为 .17. 若方程 是关于x的一元二次方程,则m=.18. 如图,抛物线 与 交于点 ,过点 作 轴的平行线,分别交两条抛物线于点 , .则以下结论:①无论 取何值, 2的值总是正数;② ;③当 时, ;④ .其中正确结论是 .
三、解答题
-
19. 解方程(1)、 (配方法)(2)、(3)、 (公式法)(4)、20. “低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2020年起逐月增加,据统计该商城1月份销售自行车64辆,3月份销售了100辆.求这个运动商城这两个月的月平均增长率是多少?21. 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形, 的三个顶点都在格点上.
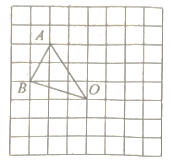 (1)、以 为原点建立直角坐标系,点 的坐标为 ,则点 的坐标为;(2)、画出 绕点 顺时针旋转90°后的22. 已知关于x的方程kx2-(3k-1)x+2(k-1)=0.
(1)、以 为原点建立直角坐标系,点 的坐标为 ,则点 的坐标为;(2)、画出 绕点 顺时针旋转90°后的22. 已知关于x的方程kx2-(3k-1)x+2(k-1)=0.求证:无论k为何实数,方程总有实数根;
23. 已知二次函数 的图象与 轴相交于 , 两点,与 轴交于 点(如图所示),点 在二次函数的图象上,且 与 关于对称轴对称,一次函数的图象过点 : (1)、求点 的坐标;(2)、求一次函数的解析式;(3)、根据图象直接写出使一次函数值大于二次函数值的 的取值范围;24. 某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.(1)、降价前商品每月销售该商品的利润是多少元?(2)、要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?(3)、当这种商品售价定为多少元时,该商品所获的利润最大?最大利润是多少?25. 如图,二次函数 的图象交 轴于 , ,交 轴于 ,过 、 画直线.
(1)、求点 的坐标;(2)、求一次函数的解析式;(3)、根据图象直接写出使一次函数值大于二次函数值的 的取值范围;24. 某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.(1)、降价前商品每月销售该商品的利润是多少元?(2)、要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?(3)、当这种商品售价定为多少元时,该商品所获的利润最大?最大利润是多少?25. 如图,二次函数 的图象交 轴于 , ,交 轴于 ,过 、 画直线.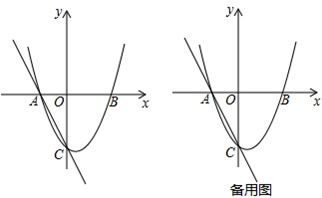 (1)、求二次函数的解析式;(2)、点 在 轴正半轴上,且 ,求 的长;(3)、若 为线段 上一个动点,过点 作 平行于 轴交抛物线于点 ,当点 运动到何处时,四边形 的面积最大?求出此时点 的坐标及四边形 面积的最大值.
(1)、求二次函数的解析式;(2)、点 在 轴正半轴上,且 ,求 的长;(3)、若 为线段 上一个动点,过点 作 平行于 轴交抛物线于点 ,当点 运动到何处时,四边形 的面积最大?求出此时点 的坐标及四边形 面积的最大值.