浙江省绍兴市新昌县2021届九年级上学期数学期中考试试卷
试卷更新日期：2020-12-14 类型：期中考试
一、单选题
-
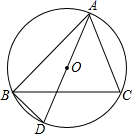
1. 下列事件中，是必然事件的是（ ）A、从一个只有红球的盒子里摸出一个球是红球 B、买一张电影票，座位号是5的倍数 C、掷一枚质地均匀的硬币，正面向上 D、走过一个红绿灯路口时，前方正好是红灯2. 下列关于二次函数y=x2﹣3的图象与性质的描述，不正确的是( )A、该函数图象的开口向上 B、函数值y随着自变量x的值的增大而增大 C、该函数图象关于y轴对称 D、该函数图象可由函数y=x2的图象平移得到3. 如图，△ABC中，∠ACB＝90°，∠ABC＝40°，将△ABC绕点B逆时针旋转得到△A'BC'，使点C的对应点C'恰好落在边AB上，则∠CAA'的度数是（ ）
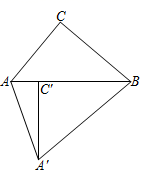A、50° B、70° C、110° D、120°4. 如图所示，圆O的弦AB垂直平分半径OC，则四边形OACB（ ）
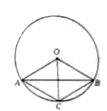A、是正方形 B、是长方形 C、是菱形 D、以上答案都不对5. 如图，点A，B，C在 上，若 ，则 ( )
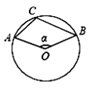A、 B、 C、 D、6. 一扇形的半径等于已知圆的半径的2倍，且它的面积等于该圆的面积，则这一扇形的圆心角为（ ）A、20° B、120° C、100° D、90°7. 某射击运动员在同一条件下的射击成绩记录如下：射击次数
20
80
100
200
400
1000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率（结果保留两位小数）
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性，估计这名运动员射击一次时“射中九环以上”的概率约是（ ）
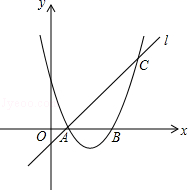
A、0.90 B、0.82 C、0.85 D、0.848. 如图，在⊙O中，直径CD⊥弦AB，则下列结论中正确的是（ ）
A、AC=AB B、2∠C=∠BOD C、∠C=∠B D、∠A=∠BOD9. 若抛物线y＝x2+bx+c与x轴只有一个公共点，且过点A（m，n），B（m﹣8，n），则n的值为（ ）A、8 B、12 C、15 D、1610. 二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：①bc＞0； ②3a+c＞0； ③a+b+c≤ax2+bx+c；④a（k12+1）2+b（k12+1）＞a（k12+2）2+b（k12+2）.其中正确结论的个数是（ ）
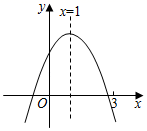A、1 B、2 C、3 D、4二、填空题
-
11. 现有下列长度的五根木棒：3，5，8，10，13，从中任取三根，可以组成三角形的概率为 ．12. 扇形 的半径为6cm，弧长为10cm，则扇形面积是.13. 如图，五边形 ABCDE 是⊙O 的内接正五边形， AF 是⊙O 的直径，则∠ BDF 的度数是°.
14. 在平面直角坐标系中，将抛物线 先向上平移3个单位长度，再向右平移2个单位长度，得到的抛物线的解析式是.15. 如图，四边形ABCD是菱形，∠A＝60°，AB＝2，扇形EBF的半径为2，圆心角为60°，则图中阴影部分的面积是.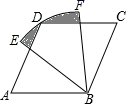
16. 如图，小滕用铁栅栏及一面墙（墙足够长）围成了一个矩形自行车场地ABCD，在AB和BC边各有一个2m宽的小门（不用铁栅栏），小滕共用了铁栅栏40米，则矩形ABCD的面积的最大值为m2.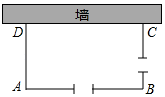
三、解答题
-
17. 有四张正面分别标有数字1，2，3，4的不透明卡片，它们除数字外无其他差别，现将它们背面朝上洗匀.(1)、随机抽取一张卡片，卡片上的数字是奇数的概率为.(2)、随机抽取一张卡片，然后放回洗匀，再随机抽取一张卡片，请用列表或画树状图的方法，求两次抽取的卡片上的数字和等于6的概率.18. 如图，△ABC的顶点坐标分别为A（0，1），B（3，3），C（1，3）.
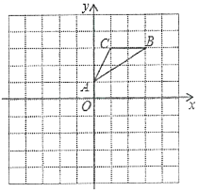
（ 1 ）画出△ABC关于点O的中心对称图形△A1B1C1.
（ 2 ）①画出△ABC绕原点O逆时针旋转90°的△A2B2C2；
②直接写出点B2的坐标为 ▲ .
19. 已知二次函数的图象经过点（0，3），顶点坐标为（1，4）.(1)、求这个二次函数的解析式；(2)、若将该抛物线绕原点旋转180°，请直接写出旋转后的抛物线函数表达式.20. 如图，△ABC是⊙O的内接三角形，点C是优弧AB上一点（点C不与点A，B重合），设∠OAB=α，∠C=β.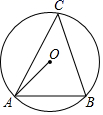
(1)、当α=40°时，求β的度数；(2)、猜想α与β之间的关系，并给予证明.21. 某商品的进价为每件20元，售价为每件25元时，每天可卖出250件.市场调查反映：如果调整价格，一件商品每涨价1元，每天要少卖出10件.(1)、求出每天所得的销售利润w(单位：元)与每件涨价x(单位：元)之间的函数关系式；(2)、求销售单价为多少元时，该商品每天的销售利润最大；(3)、商场的营销部在调控价格方面，提出了A，B两种营销方案.方案A：每件商品涨价不超过5元；
方案B：每件商品的利润至少为16元.
请比较哪种方案的最大利润更高，并说明理由.
22. 某校计划组建航模、摄影、乐器、舞蹈四个课外活动小组，要求每名同学必须参加，并且只能选择其中一个小组.为了解学生对四个课外活动小组的选择情况，学校从全体学生中随机抽取部分学生进行问卷调查，并把此次调查结果整理并绘制成如下两幅不完整的统计图.
根据图中提供的信息，解答下列问题：
(1)、本次被调查的学生有人；(2)、请补全条形统计图，并求出扇形统计图中“航模”所对应的圆心角的度数；(3)、通过了解，喜爱“航模”的学生中有2名男生和2名女生曾在市航模比赛中获奖，现从这4个人中随机选取2人参加省青少年航模比赛，请用列表或画树状图的方法求出所选的2人恰好是1名男生和1名女生的概率.
