四川省成都邛崃市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-14 类型:期中考试
一、单选题
-
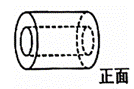
1. 如图是一个空心圆柱体,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,白炽灯下有一个乒乓球,当乒乓球越接近灯泡时,它在地面上的影子( )
2. 如图,白炽灯下有一个乒乓球,当乒乓球越接近灯泡时,它在地面上的影子( )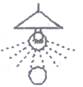 A、越大 B、越小 C、不变 D、无法确定3. 已知点(3,﹣4)在反比例函数 的图象上,则下列各点也在该反比例函数图象上的是( )A、(3,4) B、(﹣3,﹣4) C、(﹣2,6) D、(2,6)4. 某厂通过改进工艺降低了某种产品的成本,两个月内从每件产品250元降低到每件160元,则平均每月降低的百分率为( )A、10% B、5% C、15% D、20%5. 已知 ,那么 的值为( )A、 B、 C、 D、6. 在△ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )A、= B、= C、= D、=7. 如图,在 中, , , ,将 沿图示中的虚线 剪开,剪下的三角形与原三角形不相似的是( )
A、越大 B、越小 C、不变 D、无法确定3. 已知点(3,﹣4)在反比例函数 的图象上,则下列各点也在该反比例函数图象上的是( )A、(3,4) B、(﹣3,﹣4) C、(﹣2,6) D、(2,6)4. 某厂通过改进工艺降低了某种产品的成本,两个月内从每件产品250元降低到每件160元,则平均每月降低的百分率为( )A、10% B、5% C、15% D、20%5. 已知 ,那么 的值为( )A、 B、 C、 D、6. 在△ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )A、= B、= C、= D、=7. 如图,在 中, , , ,将 沿图示中的虚线 剪开,剪下的三角形与原三角形不相似的是( )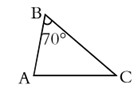 A、
A、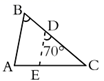 B、
B、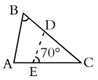 C、
C、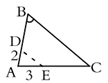 D、
D、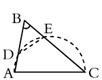 8. 已知关于x的一元二次方程 有实数根,则m的取值范围是( )A、 B、 C、 D、9. 如图, 是线段 的黄金分割点,且 ,若 表示以 为一边的正方形的面积, 表示长为 ,宽为 的矩形的面积,则 与 的大小关系是( )
8. 已知关于x的一元二次方程 有实数根,则m的取值范围是( )A、 B、 C、 D、9. 如图, 是线段 的黄金分割点,且 ,若 表示以 为一边的正方形的面积, 表示长为 ,宽为 的矩形的面积,则 与 的大小关系是( )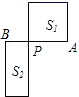 A、 B、 C、 D、无法确定10.
A、 B、 C、 D、无法确定10.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
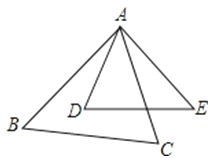 A、= B、= C、= D、=
A、= B、= C、= D、=二、填空题
-
11. 已知a是方程2x2﹣x﹣4=0的一个根,则代数式4a2﹣2a+1的值为 .12. 已知 ,则 =.13. 某种油菜籽在相同条件下发芽试验的结果如下:
每批粒数
50
100
300
400
600
1000
发芽的频数
45
96
283
380
571
948
这种油菜籽发芽的概率的估计值是.(结果精确到0.01)
14. 在平面直角坐标系中,将 以点 为位似中心, 为位似比作位似变换,得到 .已知 ,则点 的坐标是 . 15. 方程 的两根为 、 则 的值为.16. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是 .17. 如果关于 的不等式组 的解集为 ,且关于 的分式方程 的解是非负数,则所有符合条件的整数 的值之和是 .18. 如图,点 在双曲线 ( )上,过点 作 轴,垂足为点 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 交 轴于点 ,交 轴于点 ,连接 .若 ,则 的值为.
15. 方程 的两根为 、 则 的值为.16. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是 .17. 如果关于 的不等式组 的解集为 ,且关于 的分式方程 的解是非负数,则所有符合条件的整数 的值之和是 .18. 如图,点 在双曲线 ( )上,过点 作 轴,垂足为点 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 交 轴于点 ,交 轴于点 ,连接 .若 ,则 的值为. 19. 如图,在正方形ABCD中,以CD为底边作等腰 ,使得点E在正方形ABCD内部,且 ,连接BD交CE于点F . 过点C作 于点G , 过点G作 于点H , 连接HF . 若 , ,则四边形AEFH的面积为 .
19. 如图,在正方形ABCD中,以CD为底边作等腰 ,使得点E在正方形ABCD内部,且 ,连接BD交CE于点F . 过点C作 于点G , 过点G作 于点H , 连接HF . 若 , ,则四边形AEFH的面积为 .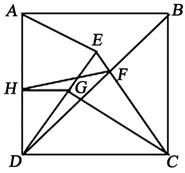
三、解答题
-
20.(1)、计算:(2)、解不等式组 ,并利用数轴确定不等式组的解集.
 21. 化简:22. 抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
21. 化简:22. 抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题: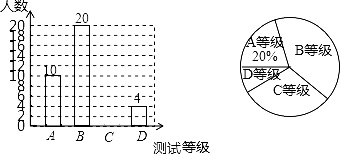 (1)、本次抽样调查共抽取了多少名学生?(2)、求测试结果为C等级的学生数,并补全条形图;(3)、若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?(4)、若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.23. 在平面直角坐标系中, 的三个顶点的坐标分别是 , , .
(1)、本次抽样调查共抽取了多少名学生?(2)、求测试结果为C等级的学生数,并补全条形图;(3)、若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?(4)、若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.23. 在平面直角坐标系中, 的三个顶点的坐标分别是 , , . (1)、画出 关于 轴成轴对称的 ;(2)、画出 以点O为位似中心,位似比为 的 .并写出 的坐标.24. 已知一次函数y=kx+b的图象与反比例函数y=- 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:
(1)、画出 关于 轴成轴对称的 ;(2)、画出 以点O为位似中心,位似比为 的 .并写出 的坐标.24. 已知一次函数y=kx+b的图象与反比例函数y=- 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求: (1)、一次函数的解析式;(2)、△AOB的面积;(3)、直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.25. 如图所示,在矩形MBCN中,点A是边MN的中点, , .点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE , 设运动时间为 ,解答下列问题:
(1)、一次函数的解析式;(2)、△AOB的面积;(3)、直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.25. 如图所示,在矩形MBCN中,点A是边MN的中点, , .点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE , 设运动时间为 ,解答下列问题: (1)、求证: ;(2)、当t为何值时, 的面积为7.5cm2;(3)、在点D , E的运动中,是否存在时间t , 使得 与 相似?若存在,请求出对应的时间t;若不存在,请说明理由.26. 商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价1元,商场平均每天可多售出2件.(1)、若某天该商品每件降价3元,当天可获利多少元?(2)、设每件商品降价x元,则商场日销售量增加件,每件商品,盈利元(用含x的代数式表示);(3)、在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到2000元?27. 几何探究题
(1)、求证: ;(2)、当t为何值时, 的面积为7.5cm2;(3)、在点D , E的运动中,是否存在时间t , 使得 与 相似?若存在,请求出对应的时间t;若不存在,请说明理由.26. 商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价1元,商场平均每天可多售出2件.(1)、若某天该商品每件降价3元,当天可获利多少元?(2)、设每件商品降价x元,则商场日销售量增加件,每件商品,盈利元(用含x的代数式表示);(3)、在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到2000元?27. 几何探究题 (1)、发现:在平面内,若 , ,其中 .
(1)、发现:在平面内,若 , ,其中 .当点A在线段BC上时,线段AC的长取得最小值,最小值为;
当点A在线段CB延长线上时,线段AC的长取得最大值,最大值为 .
(2)、应用:点A为线段BC外一动点,如图2,分别以AB、AC为边,作等边△ABD和等边△ACE , 连接CD、BE .①证明: ;
②若 , ,则线段BE长度的最大值为 .
(3)、拓展:如图3,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 ,点P为线AB外一动点,且 , , .请直接写出线段AM长的最大值及此时点P的坐标.28. 如图,平行四边形ABCD的顶点A在y轴上,点B、C在x轴上;OA、OB长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB , BC=6; (1)、写出点D的坐标;(2)、若点E为x轴上一点,且S△AOE= ,
(1)、写出点D的坐标;(2)、若点E为x轴上一点,且S△AOE= ,①求点E的坐标;
②判断△AOE与△AOD是否相似并说明理由;
(3)、若点M是坐标系内一点,在直线AB上是否存在点F , 使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.