浙江省杭州市余杭区2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-12-14 类型:期中考试
一、单选题
-
1. 如图, 内接于 ,若 ,则 的度数是( )
 A、 B、 C、 D、2. 将抛物线 向右平移1个单位,再向上平移3个单位,得到的抛物线是( )A、 B、 C、 D、3. 已知⊙O的半径为2,点P在⊙O内,则OP的长可能是( )A、1 B、2 C、3 D、44. 下列是有关圆的一些结论,其中正确的是( )A、任意三点可以确定一个圆 B、相等的圆心角所对的弧相等 C、平分弦的直径垂直于弦 D、圆内接四边形对角互补5. 已知四点 , , , ,若一个二次函数的图象经过这四点中的三点,则这个二次函数图象的对称轴为( )A、 B、 C、 D、6. 如图,在⊙O中,∠AOC=140°,∠ACB=50°,则∠BAC的度数为( )
A、 B、 C、 D、2. 将抛物线 向右平移1个单位,再向上平移3个单位,得到的抛物线是( )A、 B、 C、 D、3. 已知⊙O的半径为2,点P在⊙O内,则OP的长可能是( )A、1 B、2 C、3 D、44. 下列是有关圆的一些结论,其中正确的是( )A、任意三点可以确定一个圆 B、相等的圆心角所对的弧相等 C、平分弦的直径垂直于弦 D、圆内接四边形对角互补5. 已知四点 , , , ,若一个二次函数的图象经过这四点中的三点,则这个二次函数图象的对称轴为( )A、 B、 C、 D、6. 如图,在⊙O中,∠AOC=140°,∠ACB=50°,则∠BAC的度数为( ) A、20° B、30° C、40° D、50°7. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球,若随机摸出一个蓝球的概率为 ,则随机摸出一个红球的概率为( )A、 B、 C、 D、8. 半径相等的圆的内接正三角形、正方形、正六边形的边长之比为( )A、1: : B、 : :1 C、3:2:1 D、1:2:39. 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.P是直径MN上一动点,则PA+PB的最小值为( )
A、20° B、30° C、40° D、50°7. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球,若随机摸出一个蓝球的概率为 ,则随机摸出一个红球的概率为( )A、 B、 C、 D、8. 半径相等的圆的内接正三角形、正方形、正六边形的边长之比为( )A、1: : B、 : :1 C、3:2:1 D、1:2:39. 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.P是直径MN上一动点,则PA+PB的最小值为( )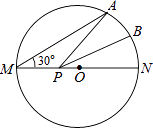 A、 B、1 C、2 D、210. 已知点P在函数 图象上,点P关于x轴的对称点在函数 的图象上,则实数a的取值范围是( ).A、 B、 C、 D、
A、 B、1 C、2 D、210. 已知点P在函数 图象上,点P关于x轴的对称点在函数 的图象上,则实数a的取值范围是( ).A、 B、 C、 D、二、填空题
-
11. 小明用0﹣9中的数字给手机设置了六位开机密码,但他把最后一位数字忘记了,小明只输入一次密码就能打开手机的概率是.12. 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=10,AE=1,则弦CD的长是.
 13. 如图,在⊙O中,弦AC、BD相交于点E,且 ,若∠BEC=130°,则∠ACD的度数为
13. 如图,在⊙O中,弦AC、BD相交于点E,且 ,若∠BEC=130°,则∠ACD的度数为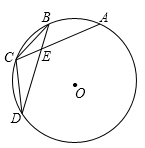 14. 若一条弦分圆为1:4两部分,则这条弦所对的圆周角的度数是.15. 如图,抛物线 与x轴相交于 两点,其中 ,当 时,y0(填“>”“=”或“<”号).
14. 若一条弦分圆为1:4两部分,则这条弦所对的圆周角的度数是.15. 如图,抛物线 与x轴相交于 两点,其中 ,当 时,y0(填“>”“=”或“<”号). 16. 如图, 内接于半径为 的半圆,AB为直径,点M是弧AC的中点,连结BM交AC于点E,AD平分∠CAB交BM于点D,∠ADB=°,当点D恰好为BM的中点时,BM的长为.
16. 如图, 内接于半径为 的半圆,AB为直径,点M是弧AC的中点,连结BM交AC于点E,AD平分∠CAB交BM于点D,∠ADB=°,当点D恰好为BM的中点时,BM的长为.
三、解答题
-
17. 若二次函数 的x与y的部分对应值如下表:
x
-1
0
1
2
3
4
y
0
3
4
3
0
-5
(1)、求这个二次函数的表达式;(2)、当x=﹣2时,y的值.18. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机摸取一个小球然后放回,再随机摸出一个小球,请用树状图或列表法求下列事件的概率.(1)、两次取出的小球的标号相同;(2)、两次取出的小球标号的和等于6.19. 如图,在平面直角坐标系 中,点 ,点 ,点 ,以点C为中心,把 逆时针旋转 后得到 .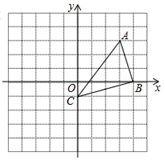 (1)、写出点 、 的坐标,并画出旋转后的图形 ;(2)、求点A经过的路径弧 的长(结果保留 ).20. 如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E , 连接AD , BC , CO
(1)、写出点 、 的坐标,并画出旋转后的图形 ;(2)、求点A经过的路径弧 的长(结果保留 ).20. 如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E , 连接AD , BC , CO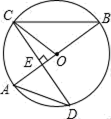 (1)、当∠BCO=25°时,求∠A的度数;(2)、若CD=4 ,BE=4,求⊙O的半径.21. 如图,斜坡 长10米,按图中的直角坐标系可用 表示,点A,B分别在x轴和y轴上.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛线可用 表示.
(1)、当∠BCO=25°时,求∠A的度数;(2)、若CD=4 ,BE=4,求⊙O的半径.21. 如图,斜坡 长10米,按图中的直角坐标系可用 表示,点A,B分别在x轴和y轴上.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛线可用 表示. (1)、求抛物线的表达式及顶点坐标;(2)、在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?
(1)、求抛物线的表达式及顶点坐标;(2)、在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?
