陕西省榆林市子洲县2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-12-14 类型:期中考试
一、单选题
-
1. 若a , b , c , d是成比例线段,其中a=3cm , c=6cm , d=4cm , 则b等于( )A、8 cm B、 cm C、4 cm D、2cm2. 已知△ABC∽△A1B1C1 , 且∠A=60°,∠B1=40°,则∠C1的度数为( )A、40° B、60° C、80° D、100°3. 已知方程 的一个根是2,则k的值是 ( )A、 B、 C、 D、4. 如图,公路 、 互相垂直,公路 的中点M与点C被湖隔开,若测得 的长为 ,则M、C两点间的距离为( )
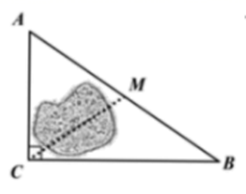 A、 B、 C、 D、5. 用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,是指( )A、连续掷2次,结果一定是“正面朝上”和“反面朝上”各1次 B、连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次 C、抛掷2n次硬币,恰好有n次“正面朝上” D、抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.56. 已知菱形 中,对角线 与 交于点O, , ,则该菱形的周长是( )
A、 B、 C、 D、5. 用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,是指( )A、连续掷2次,结果一定是“正面朝上”和“反面朝上”各1次 B、连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次 C、抛掷2n次硬币,恰好有n次“正面朝上” D、抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.56. 已知菱形 中,对角线 与 交于点O, , ,则该菱形的周长是( ) A、13 B、52 C、120 D、2407. 如图,在平面直角坐标系中, 的顶点坐标分别是 , , ,以原点为位似中心,在原点的同侧画 ,使 与 成位似图形,且相似比为 ,则线段 的长度为( )
A、13 B、52 C、120 D、2407. 如图,在平面直角坐标系中, 的顶点坐标分别是 , , ,以原点为位似中心,在原点的同侧画 ,使 与 成位似图形,且相似比为 ,则线段 的长度为( ) A、 B、2 C、4 D、58. 受益于电子商务的发展以及法治环境的改善等多重因素,快递业成为我国经济的一匹“黑马”2018年我国快递业务量为507亿件,2020年快递量将达到700亿件,设快递量平均每年增长率为x.则下列方程中正确的是( )A、 B、 C、 D、9. 如图,平行四边形ABCD中,F是CD上一点,BF交AD的延长线于G,则图中的相似三角形对数共有( )
A、 B、2 C、4 D、58. 受益于电子商务的发展以及法治环境的改善等多重因素,快递业成为我国经济的一匹“黑马”2018年我国快递业务量为507亿件,2020年快递量将达到700亿件,设快递量平均每年增长率为x.则下列方程中正确的是( )A、 B、 C、 D、9. 如图,平行四边形ABCD中,F是CD上一点,BF交AD的延长线于G,则图中的相似三角形对数共有( ) A、8对; B、6对; C、4对; D、2对.10. 如图,四边形 是边长为2的正方形点P为线段 上的动点,E为 的中点,射线 交 的延长线于点Q,过点E作 的垂线交 于点H.交 的延长线于点F,则以下结论:① ;② ;③当点F与点C重合时 ;④当 时, .成立的是( )
A、8对; B、6对; C、4对; D、2对.10. 如图,四边形 是边长为2的正方形点P为线段 上的动点,E为 的中点,射线 交 的延长线于点Q,过点E作 的垂线交 于点H.交 的延长线于点F,则以下结论:① ;② ;③当点F与点C重合时 ;④当 时, .成立的是( )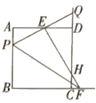 A、①②③ B、①③④ C、②③④ D、②④
A、①②③ B、①③④ C、②③④ D、②④二、填空题
-
11. 方程 的根是.12. 如图,直线 ,直线 和 被 , , 所截, , , ,则 的长为.
 13. 为了防控输入性“新冠肺炎”,某医院成立隔离治疗发热病人防控小组,决定从内科3位骨干医师中(含有甲)抽调2人组成,则甲一定会被抽调到防控小组的概率是.14. 如图,矩形 中, , ,点P是 边上动点,则 的最小值为.
13. 为了防控输入性“新冠肺炎”,某医院成立隔离治疗发热病人防控小组,决定从内科3位骨干医师中(含有甲)抽调2人组成,则甲一定会被抽调到防控小组的概率是.14. 如图,矩形 中, , ,点P是 边上动点,则 的最小值为.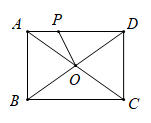
三、解答题
-
15. 解方程: .16. 一个口袋中放有16个球,其中红球6个,白球和黑球各若干个,每个球除了颜色外没有任何区别.小明通过大量反复的试验(每次将球搅匀后,任意摸出一个球记下颜色后再放回)发现,取出黑球的频率稳定在 附近,请你估计袋中白球的个数17. 如图,四边形 是正方形,对角线 、 相交于点F, , .求证:四边形 是正方形.
 18. 已知关于x的一元二次方程 .求证:无论k为何实数,方程总有两个不相等的实数根.19. 如图,在 中, 为 的中点,连接 并延长交 的延长线于点F,连接 , ,若 ,判断四边形 的形状,并说明理由.
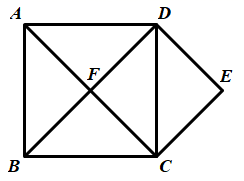
18. 已知关于x的一元二次方程 .求证:无论k为何实数,方程总有两个不相等的实数根.19. 如图,在 中, 为 的中点,连接 并延长交 的延长线于点F,连接 , ,若 ,判断四边形 的形状,并说明理由. 20. 大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列入第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆 ,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得 米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与大雁塔底处的点A在同一直线上),这时测得 米, 米,请你根据以上数据,计算大雁塔的高度 .
20. 大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列入第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆 ,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得 米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与大雁塔底处的点A在同一直线上),这时测得 米, 米,请你根据以上数据,计算大雁塔的高度 .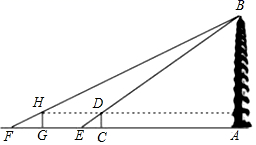 21. 如图,在 中点D,E,F分别在 , , 边上, , .
21. 如图,在 中点D,E,F分别在 , , 边上, , .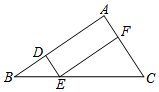 (1)、求证: ;(2)、若 , 的面积是20,求 的面积.22. “十一期间”,美美家电商场举行了买家电进行“翻牌抽奖”的活动其规则为:现准备有4张牌,4张牌分别对应100,200,300,400(单位:元)的现金.(1)、如果某位顾客随机翻1张牌,那么这位顾客抽中200元现金的概率为.(2)、如果某位顾客随机翻2张牌,且第一次翻过的牌需放回洗匀后再参加下次翻牌,用列表法或画树状图求该顾客所获现金总额不低于500元的概率.23. 某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米.
(1)、求证: ;(2)、若 , 的面积是20,求 的面积.22. “十一期间”,美美家电商场举行了买家电进行“翻牌抽奖”的活动其规则为:现准备有4张牌,4张牌分别对应100,200,300,400(单位:元)的现金.(1)、如果某位顾客随机翻1张牌,那么这位顾客抽中200元现金的概率为.(2)、如果某位顾客随机翻2张牌,且第一次翻过的牌需放回洗匀后再参加下次翻牌,用列表法或画树状图求该顾客所获现金总额不低于500元的概率.23. 某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米. (1)、为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?(2)、如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽为多少米?
(1)、为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?(2)、如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽为多少米?

