陕西省咸阳市武功县2021届九年级上学期数学期中考试试卷
试卷更新日期：2020-12-14 类型：期中考试
一、单选题
-
1. 方程 x2=x 的根是（ ）A、x=1 B、x=﹣1 C、x1=0，x2=1 D、x1=0，x2=﹣12. 下列命题中，不正确的是（ ）A、对角线相等且垂直的四边形是正方形 B、有一个角是直角的菱形是正方形 C、顺次连接菱形各边中点所得的四边形是矩形 D、有一个角是 的等腰三角形是等边三角形3. 如图， 、 是锐角 两边 、 上的高，它们交于点D，图中共有几对相似三角形（ ）
A、3对 B、4对 C、5对 D、6对4. 一种药品经两次降价，由每盒50元调至40.5元，平均每次降价的百分率是（ ）A、5% B、10% C、15% D、20%5. 如图，正方形ABCD的边长为1，点E，F分别是对角线AC上的两点，EG⊥AB．EI⊥AD，FH⊥AB，FJ⊥AD，垂足分别为G，I，H，J．则图中阴影部分的面积等于 （ ）
A、1 B、 C、 D、6. 若关于 的一元二次方程 的常数项为0，则m的值等于（ ）A、1 B、2 C、1或2 D、07. 如图，在平面直角坐标系中，▱MNEF的两条对角线ME ， NF交于原点O ， 点F的坐标是(3，2)，则点N的坐标为（ ）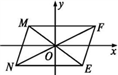
A、(-3，-2) B、(-3，2) C、(-2，3) D、(2，3)8. 如图，用两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色，那么可配成紫色的概率是（ ）
A、 B、 C、 D、9. 如图，AB和CD表示两根直立于地面的柱子，AC和BD表示起固定作用的两根钢筋，AC与BD相交于点M，已知AB=8m，CD=12m，则点M离地面的高度MH为（ ）
A、4 m B、 m C、5m D、 m10. 如图，在周长为20cm的平行四边形ABCD中，AB≠AD，AC和BD相交于点O，OE⊥BD交AD于E，则ΔABE的周长为（ ）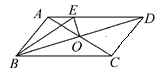
A、4cm B、6cm C、8cm D、10cm二、填空题
-
11. 如图， 和 中， ，请添加一个适当的条件 ， 使 ∽ （只填一个即可）.
12. 若菱形ABCD的边长为13cm，对角线BD长10cm，则菱形ABCD的面积是cm2.13. 观察表格，一元二次方程x2﹣x﹣1.1=0最精确的一个近似解是（精确到0.1）．x
1.3
1.4
1.5
1.6
1.7
1.8
1.9
x2﹣x﹣1.1
﹣0.71
﹣0.54
﹣0.35
﹣0.14
0.09
0.34
0.61
14. 在一次新年聚会中，小朋友们互相赠送礼物，全部小朋友共互赠了110件礼物，若假设参加聚会小朋友的人数为x人，则根据题意可列方程为.三、解答题
-
15. 解方程： .16. 如图，E、F为平行四边形 对角线 上的两点，且 ，连接 、 ，求证： .
17. 如图，小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边DE=40cm.EF=30cm，测得边DF离地面的高度AC=1.5m，CD=10m，求树高AB.
18. 列一元二次方程解应用题某公司今年1月份的纯利润是20万元，由于改进技术，生产成本逐月下降，3月份的纯利润是22.05万元.假设该公司2、3、4月每个月增长的利润率相同.
(1)、求每个月增长的利润率；(2)、请你预测4月份该公司的纯利润是多少？19. 在等腰△ABC中，三边分别为a、b、c，其中a=5，若关于x的方程x2+（b+2）x+6﹣b=0有两个相等的实数根，求△ABC的周长．20. 国庆节假日期间，昀昀一家去公园游玩，在一个场所有一个“守株待兔”的游戏，游戏设计者提供了一只兔子和一个有A、B、C、D四个出入口的兔笼，而且笼内的兔子从每个出入口走出兔笼的机会是均等的.游戏规定：①玩家只能将小兔从A、B两个出入口放入；②如果小兔进入笼子后选择从开始进入的出入口离开，则可获得一只价值4元的小兔玩具，否则应付费3元.(1)、画树状图或列表格，写出该游戏的所有可能结果；(2)、昀昀玩该游戏得到小兔玩具的机会有多大？(3)、假设有120人次玩此游戏，估计游戏设计者可赚多少钱？21. 如图，在正方形ABCD中，E为边AD的中点，点F在边CD上，且∠BEF＝90°，延长EF交BC的延长线于点G；
(1)、求证：△ABE∽△EGB；(2)、若AB＝4，求CG的长.22. 如图，在一个可以自由转动的转盘中，指针位置固定，三个扇形的面积都相等，且分别标有数字1，2，3．
(1)、小明转动转盘一次，当转盘停止转动时，指针所指扇形中的数字是奇数的概率为；
(2)、小明先转动转盘一次，当转盘停止转动时，记录下指针所指扇形中的数字；接着再转动转盘一次，当转盘停止转动时，再次记录下指针所指扇形中的数字，求这两个数字之和是3的倍数的概率（用画树状图或列表等方法求解）．23.如图，△ABC≌△ABD，点E在边AB上，CE∥BD，连接DE．求证：
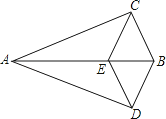(1)、∠CEB=∠CBE；(2)、四边形BCED是菱形
24. 某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件．(1)、降价前商场每月销售该商品的利润是多少元？(2)、要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？25. 在四边形 ABCD 中，对角线 AC、BD 相交于点 O，过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H.
(1)、如图①，若四边形 ABCD 是正方形，且 AG＝BE＝CH＝DF，则 S四边形AEOG＝S正方形 ABCD；(2)、如图②，若四边形 ABCD 是矩形，且 S四边形 AEOG＝ S矩形 ABCD ， 设 AB＝a， AD＝b，BE＝m，求 AG 的长（用含 a、b、m 的代数式表示）；(3)、如图③，若四边形 ABCD 是平行四边形，且 AB＝3，AD＝5，BE＝1， 试确定 F、G、H 的位置，使直线 EF、GH 把四边形 ABCD 的面积四等分.