湖南省长沙市周南教育集团2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2020-12-14 类型：期中考试

进入出卷网下载

一、单选题

1. 在0，2， $\frac{1}{2}$ ，﹣1， $- \frac{1}{2}$ 这五个数中，最小的数是（）

A、0 B、2 C、 $- \frac{1}{2}$ D、﹣1

查看试题解析
2. 下列图形，是轴对称图形但不是中心对称图形的是（）

A、等边三角形 B、平行四边形 C、圆 D、正方形

查看试题解析
3. 截止到2020年10月23日，电影《我和我的家乡》的累计票房达到了2536000000元，2536000000用科学记数法表示为（）

A、 $25.36 \times 10^{9}$ B、 $2.536 \times 10^{9}$ C、 $2.536 \times 10^{5}$ D、 $253.6 \times 10^{5}$

查看试题解析
4. 下列运算正确的是（）

A、 ${(x + y)}^{2} = x^{2} + y^{2}$ B、 ${(x^{2})}^{2} = x^{3}$ C、 $x^{3} \cdot x^{3} = x^{6}$ D、 $x^{6} \div x^{3} = x^{2}$

查看试题解析
5. 分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则（）

A、 $x = 2$ B、 $x = \pm 2$ C、 $x = - 2$ D、 $x = 0$

查看试题解析
6. 下列说法正确的是（）

A、三点确定一个圆 B、度数相等的弧是等弧 C、三角形内心到三边的距离相等 D、垂直于半径的直线是圆的切线

查看试题解析
7. 如图，DE∥BC ， BE平分∠ABC ，若∠1＝70°，则∠CBE的度数为（　　）

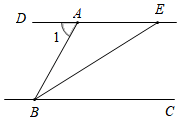A、20° B、35° C、55° D、70°

查看试题解析
8. 关于x的一元二次方程 $x^{2} - 2 x - k = 0$ 有实数根，则k的取值范围在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，在⊙O中，半径OC与弦AB垂直于点D ，且 $A B = 8$ ， $O D = 3$ ，则OC的长是（）

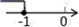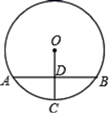A、2 B、3 C、4 D、5

查看试题解析
10. 如图，在△ABC中，∠C＝67°，将△ABC绕点A顺时针旋转后，得到△AB′C′，且点C′在BC上，则∠B′C′B的度数为（）

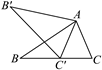A、56° B、50° C、46° D、40°

查看试题解析
11. 国家决定对某药品价格分两次降价，若设平均每次降价的百分率为x ，该药品原价为18元，降价后的价格为y元，则y与x的函数关系式为（）

A、 $y = 36 (1 - x)$ B、 $y = 36 (1 + x)$ C、 $y = 18 {(1 - x)}^{2}$ D、 $y = 18 (1 - x^{2})$

查看试题解析
12. 如图，⊙O是以原点为圆心， $\sqrt{2}$ 为半径的圆，点 $P$ 是直线 $y = - x + 6$ 上的一点，过点 $P$ 作⊙O的一条切线PQ ， Q为切点，则切线长PQ的最小值为（）

A、3 B、4 C、 $6 - \sqrt{2}$ D、 $3 \sqrt{2} - 1$

查看试题解析

二、填空题

13. 若1是 $x^{2} - 2 a x + 3 = 0$ 的解，则 $a =$ ．

查看试题解析
14. 已知圆锥的底面半径为3，母线长为7，则圆锥的侧面积是.

查看试题解析
15. 如图，在平行四边形 $A B C D$ 中， $A B = 6$ ， $A D = 8$ ， $∠ B A D = 120 °$ ，分别以点 $A$ ， $B$ 为圆心，以大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于点 $P$ 、 $Q$ ，作直线 $P Q$ ，交 $A B$ 于点 $E$ ，交 $B C$ 于点 $F$ ，则 $C F$ 的长为.

查看试题解析
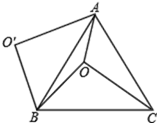
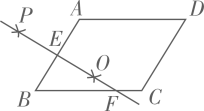16. 如图，O是正△ABC内一点， $O A = 3$ ， $O B = 4$ ， $O C = 5$ ，将线段BO以点B为旋转中心逆时针旋转60°得到线段 $B O^{'}$ ，下列结论正确的有． (请填序号)
①点O与 $O^{'}$ 的距离为4；② $∠ A O B = 150 °$ ；③ $S_{四边形 A O B O^{'}} = 6 + 3 \sqrt{3}$ ；④ $S_{△ A O C} + S_{△ A O B} = 6 + \frac{9}{4} \sqrt{3}$ ．

查看试题解析

三、解答题

17. 计算： $\sqrt{{(- 3)}^{2}} - | \sqrt{3} - 2 | + {(- \frac{1}{3})}^{- 2} - {(2020 - π)}^{0}$ ．

查看试题解析
18. 先化简，再求值： $\frac{1}{x^{2} - x} - \frac{x - 2}{x^{2} - 2 x + 1} \div \frac{x - 2}{x - 1}$ ，其中x= $\sqrt{3}$ ．

查看试题解析
19. 解不等式组 ${\begin{array}{l} x + 4 < 3 \\ \frac{1 - x}{3} \leq 1 \end{array}$ ．

查看试题解析
20. 中考体育测试前，某区教育局为了了解选报引体向上的初三男生的成绩情况，随机抽测了本区部分选报引体向上项目的初三男生的成绩，并将测试得到的成绩绘成了下面两幅不完整的统计图：
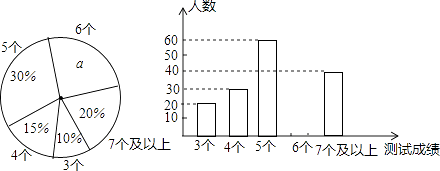
请你根据图中的信息，解答下列问题：

(1)、写出扇形图中a=%，并补全条形图；

(2)、在这次抽测中，测试成绩的众数和中位数分别是个、个．

(3)、该区体育中考选报引体向上的男生共有1800人，如果体育中考引体向上达6个以上（含6个）得满分，请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名？

查看试题解析
21. 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为 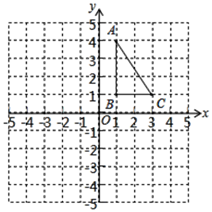$A (1 ， 4)$ ， $B (1 ， 1)$ ， $C (3 ， 1)$ ．

(1)、画出△ABC关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、画出△ABC绕B点顺时针旋转90°后的 $△ A_{2} B_{2} C_{2}$ ，求 $A_{2}$ 、 $B_{2}$ 、 $C_{2}$ 的坐标．

查看试题解析
22. 在“新冠”疫情期间，全国人民“众志成城，同心抗疫”，某商家决定将一周获得的利润全部捐赠给社区用于抗疫．已知商家购进一批产品，成本为10元/件，拟采取线上和线下两种方式进行销售．调查发现，线下的周销售量y(单位：件)与线下售价x(单位：元/件， $12 \leq x < 24$ )满足一次函数的关系，部分数据如下表：

x(元/件)

12

13

14

15

16

y(件)

120

110

100

90

80

(1)、求y与x的函数关系式；

(2)、若线上售价始终比线下每件便宜2元，且线上的周销售量固定为40件．试问：当x为多少时，线上和线下周利润总和达到最大？并求出此时的最大利润．

查看试题解析
23. 如图已知AB是⊙O的直径， $A B = 10$ ，点C ， D在⊙O上，DC平分∠ACB ，点E在⊙O外， $∠ E A C = ∠ D$ ．

(1)、求证：AE是⊙O的切线；

(2)、求AD的长．

查看试题解析
24. 有两个内角分别是它们对角的一半的四边形叫做半对角四边形

(1)、如图1，在半对角四边形ABCD中，∠B= $\frac{1}{2}$ ∠D，∠C= $\frac{1}{2}$ ∠A，求∠B与∠C的度数之和；

(2)、如图2，锐角△ABC内接于⊙O，若边AB上存在一点D，使得BD=BO，∠OBA的平分线交OA于点E，连结DE并延长交AC于点F，∠AFE=2∠EAF．求证：四边形DBCF是半对角四边形；

(3)、如图3，在（2）的条件下，过点D作DG⊥OB于点H，交BC于点G，当DH=BG=2时，求⊙O的直径．

查看试题解析
25. 已知抛物线y=ax²+bx+3经过A(−3，0)，B(−1，0)两点(如图1)，顶点为M.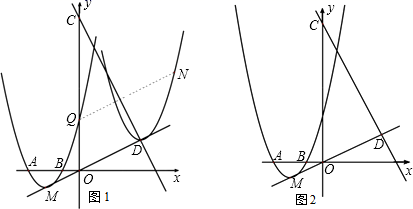

(1)、a、b的值；

(2)、设抛物线与y轴的交点为Q(如图1)，直线y=−2x+9与直线OM交于点D．现将抛物线平移，保持顶点在直线OD上.当抛物线的顶点平移到D点时，Q点移至N点，求抛物线上的两点M、Q间所夹的曲线MQˆ扫过的区域的面积；

(3)、设直线y=−2x+9与y轴交于点C，与直线OM交于点D(如图2).现将抛物线平移，保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)没有公共点时，试探求其顶点的横坐标h的取值范围.

查看试题解析

x(元/件)	12	13	14	15	16
y(件)	120	110	100	90	80