陕西省宝鸡市金台区2021届九年级上学期数学期中考试试卷

试卷更新日期：2020-12-14 类型：期中考试

进入出卷网下载

一、单选题

1. 菱形的两条对角线分别为8和6，则菱形的周长和面积分别是 $($ 　　 $)$

A、20，48 B、14，48 C、24，20 D、20，24

查看试题解析
2. 如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120°，AB=2，则AC的长为（）

A、2 B、4 C、6 D、8

查看试题解析
3. 下列说法中不正确的是 $()$

A、四边相等的四边形是菱形 B、对角线互相垂直的平行四边形是菱形 C、矩形的对角线互相垂直且相等 D、正方形的对角线相等

查看试题解析
4. 若方程 $(m - 1) x^{m^{2} + 1} - (m + 1) x - 2 = 0$ 是关于x的一元二次方程，则m的值为（）

A、-1 B、±1 C、1 D、0

查看试题解析
5. 小明将分别标有爱我中华汉字的四个小球装在一个不透明的口袋中，这些球除汉字外都相同，每次摸球前先搅拌均匀，随机摸出一球记下汉字后放回，再随机摸出一球，两次摸出的球上的汉字能组成“中华”的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{8}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
6. 一元二次方程 $x^{2} + 4 x = 2$ 配方后化为（）

A、 ${(x + 2)}^{2} = 6$ . B、 ${(x - 2)}^{2} = 6$ C、 ${(x + 2)}^{2} = - 6$ D、 ${(x + 2)}^{2} = - 2$

查看试题解析
7. 如图，两张等宽的纸条交叉重叠在一起，重叠的部分为四边形 $A B C D$ ，若测得 $A ， C$ 之间的距离为 $3 c m$ ，点 $B ， D$ 之间的距离为 $4 c m$ ，则线段 $A B$ 的长为（）

A、 $2.5 c m$ B、 $3 c m$ C、 $3.5 c m$ D、 $4 c m$

查看试题解析
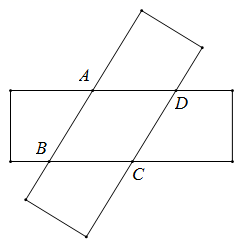8. 三角形两边的长是6和8，第三边满足方程x²﹣24x+140＝0，则三角形周长为（　　）

A、24 B、28 C、24或28 D、以上都不对

查看试题解析
9. 在元旦庆祝活动中，参加活动的同学互赠贺卡，共送贺卡42张，则参加活动的同学有（）

A、6人 B、7人 C、8人 D、9人

查看试题解析
10. 如图，在正方形 $A B C D$ 中，E为 $C D$ 边上一点，F为 $B C$ 延长线上一点，且 $C E = C F$ ，连接 $E F$ .给出下列至个结论：① $B E = D F$ ；② $B E ⊥ D F$ ；③ $E F = \sqrt{2} C F$ ；④ $∠ E D F = ∠ E B F$ ；⑤ $F D = 2 E C$ .其中正确结论的个数是（）

A、 $2 个$ B、 $3 个$ C、 $4 个$ D、 $5 个$

查看试题解析

二、填空题

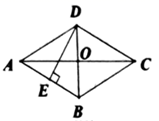
11. 若关于x的方程 $x^{2} + a x - 2 = 0$ 有一个根是1，则 $a =$ .

查看试题解析
12. 如果关于x的一元二次方程 $x^{2} - 3 x + k = 0$ 有两个相等的实数根，那么实数k的值是.

查看试题解析
13. 顺次连接矩形各边中点所得四边形为.

查看试题解析
14. 在一个不透明的袋子中装有3个白球和若干个红球，这些球除颜色外都相同.每次从袋子中随机摸出一个球，记下颜色后再放回袋中，通过多次重复试验发现摸出红球的频率稳定在0.7附近，则袋子中红球约有个.

查看试题解析
15. 某公司前年缴税 $400$ 万元，今年缴税 $484$ 万元，该公司这两年缴税的平均增长率为.

查看试题解析
16. 如图，菱形 $A B C D$ 的对角线 $A C ， B D$ 相交于点 $O ，$ 且 $A C = 2 \sqrt{3} ， B D = 2$ ，求菱形边上的高 $D E$ 为.

查看试题解析
17. 如图，正方形ABCD中，对角线AC ， BD交于点O ， E点在BC上，EG⊥OB ， EF⊥OC ，垂足分别为点G ， F ， AC＝10，则EG＋EF＝．

查看试题解析
18. 如图，将矩形 $A B C D$ 沿 $E F$ 折叠，使顶点C恰好落在 $A B$ 边的中点 $C'$ 上，点D落在 $D'$ 处， $C' D'$ 交 $A E$ 于点M.若 $A B = 6 ， B C = 9$ ，则 $B F$ 的长为

查看试题解析

三、解答题

19. 解下列一元二次方程:

(1)、 ${(x + 1)}^{2} - 25 = 0$

(2)、 $x^{2} - 4 x - 2 = 0$

(3)、 $2 x^{2} - 13 x + 15 = 0$

(4)、 $(x - 3) (x - 2) = 12$

查看试题解析
20. 尺规作图：画一个菱形，使它的两条对角线的长度分别为 $4 c m$ 和 $6 c m$ （保留作图痕迹，不写作法）

查看试题解析
21. 已知菱形ABCD中，E、F分别是CB、CD上的点，且BE=DF.

求证：

(1)、△ABE≌△ADF；

(2)、∠AEF=∠AFE

查看试题解析
22. 如图，在长为 $32 m$ ，宽为 $20 m$ 的矩形地面上，修筑同样宽的两条平行且与另一条相互垂直的道路，余下的六个空白的部分作为耕地，要使得耕地的面积为 $504 m^{2}$ ，道路的宽应为多少?

查看试题解析
23. 现有A、B两个不透明袋子，分别装有3个除颜色外完全相同的小球。其中，A袋装有2个白球，1个红球；B袋装有2个红球，1个白球。

(1)、将A袋摇匀，然后从A袋中随机取出一个小球，求摸出小球是白色的概率；

(2)、小华和小林商定了一个游戏规则：从摇匀后的A，B两袋中随机摸出一个小球，摸出的这两个小球，若颜色相同，则小林获胜；若颜色不同，则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。

查看试题解析
24. 服装柜在销售中发现某品牌童装平均每天可售出20件，每件盈利40元.为了迎接“六一”儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存.经市场调查发现，如果每件童装每降价4元，那么平均每天就可多售出8件，要想平均每天在销售这种童装上盈利1200元，那么每件童装应降价多少元？

查看试题解析
25. 如图， $△ A B C$ 中，点O是边 $A C$ 上一个动点，过O作直线 $M N // B C$ ，设 $M N$ 交 $∠ B C A$ 的平分线于点E，交 $∠ B C A$ 的外角平分线于点F.

(1)、探究：线段 $O E$ 与 $O F$ 的数量关系，并加以证明；

(2)、若 $C E = 4 ， C F = 3$ ，求 $O C$ 的长；

(3)、当点O运动到何处，且 $△ A B C$ 满足什么条件时，四边形 $A E C F$ 是正方形?并说明理由.

查看试题解析