湖南省长沙市雨花区雅礼教育集团2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2020-12-14 类型：期中考试

进入出卷网下载

一、单选题

1. 2020的相反数是（）

A、 -2020 B、2020 C、 $- \frac{1}{2020}$ D、 $\frac{1}{2020}$

查看试题解析
2. 下列计算正确的是（）

A、（a+b）²＝a²+b² B、 $2 \sqrt{3} - \sqrt{3} = 1$ C、（a²）³＝a⁶ D、a⁴÷a⁴＝0

查看试题解析
3. 2018年我市财政计划安排社会保障和公共卫生等支出约1800000000元支持民生幸福工程，数1800000000用科学记数法表示为 $($ $)$

A、 $18 \times 10^{8}$ B、 $1.8 \times 10^{8}$ C、 $1.8 \times 10^{9}$ D、 $0.18 \times 10^{10}$

查看试题解析
4. 下列说法正确的是（）

A、“明天降雨的概率为50%”，意味着明天一定有半天都在降雨 B、了解全国快递包裹产生的包装垃圾数量适合采用全面调查（普查）方式 C、反复抛一枚均匀硬币，平均每100次出现正面朝上50次 D、一组数据的方差越小，则这组数据的波动也越小

查看试题解析
5. 下列各式中正确的是 $($ $)$

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $\sqrt[3]{9} = 3$ D、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$

查看试题解析
6. 不等式组 ${\begin{matrix} x + 1 > 0 \\ 2 x - 6 \leq 0 \end{matrix}$ 的解集在数轴上表示正确的是 $($ $)$

A、 B、 C、 D、

查看试题解析
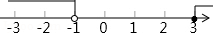7. 如图，直线a $//$ b ，直线l与a、b分别相交于A、B两点，过点A作直线l的垂线交直线b于点C ，若∠1＝60°，则∠2的度数为（）

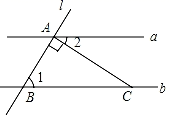A、60° B、40° C、30° D、20°

查看试题解析
8. 下列判断错误的是（　　）

A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、两条对角线垂直且平分的四边形是正方形

查看试题解析
9. 一元二次方程x²﹣3x＝4的两根分别为x₁和x₂ ，则x₁x₂为（）

A、3 B、﹣3 C、4 D、﹣4

查看试题解析
10. 在《九章算术》中有“盈不足术”的问题，原文如下：今有共买物，人出八，盈三；人出七，不足四，问人数几何？大意为：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，还差4元，问人数是多少？若设人数为 $x$ 人，则下列关于 $x$ 的方程正确的是（）

A、 $8 x - 3 = 7 x + 4$ B、 $8 (x - 3) = 7 (x + 4)$ C、 $8 x + 4 = 7 x - 3$ D、 $\frac{1}{7} x - 3 = \frac{1}{8} x + 4$

查看试题解析
11.
如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（　　）

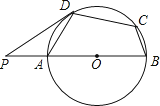A、40° B、35° C、30° D、45°

查看试题解析
12. 如图，是抛物线y₁＝ax²+bx+c（a≠0）图象的一部分，抛物线的顶点坐标是A（1，3），与x轴的一个交点B（4，0），直线y₂＝mx+n（m≠0）与抛物线交于A ， B两点，下列结论：①2a+b＝0；m+n＝3；②抛物线与x轴的另一个交点是（﹣1，0）；③方程ax²+bx+c＝3有两个相等的实数根；④当1 $<$ x $<$ 4时，有y₂ $<$ y₁；⑤若ax₁²+bx₁＝ax₂²+bx₂ ，且x₁≠x₂ ，则x₁+x₂＝1．正确的为（）

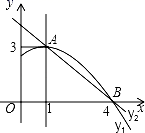A、①④⑤ B、①③④ C、①③⑤ D、①②③

查看试题解析

二、填空题

13. 如果1是方程2x²﹣x+m＝0的一个根，则m＝．

查看试题解析
14. 分式方程 $\frac{4}{x - 3} = \frac{2}{x}$ 的解为x＝．

查看试题解析
15. 已知圆锥的底面直径为6cm ，其母线长为5cm ，则它的侧面积为．

查看试题解析
16. 已知三角形三边分别为3、4、5，则该三角形内心与外心之间的距离为．

查看试题解析

三、解答题

17. 计算：|1﹣ $\sqrt{3}$ |﹣（﹣1）²⁰²⁰+（π﹣2020）⁰+（﹣ $\frac{1}{2}$ ）^-1 ．

查看试题解析
18. 先化简，再求值： $\frac{1}{x + 1} - \frac{3 - x}{x^{2} - 6 x + 9} \div \frac{x^{2} + x}{x - 3}$ ，其中x＝ $\sqrt{3}$ ．

查看试题解析
19. 如图，在平面直角坐标系中，点P（3，4），连接OP ，将线段OP绕点O顺时针旋转270°得线段OP₁ ．

(1)、在图中作出线段OP₁ ，并写出P₁点的坐标；

(2)、求点P在旋转过程中所绕过的路径长；

(3)、求线段OP在旋转过程中所扫过的图形的面积．

查看试题解析
20. “赏中华诗词，寻文化基因，品生活之美”，雅礼集团举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，根据测试成绩绘制出如图所示的部分频数分布直方图．请根据图中信息完成下列各题．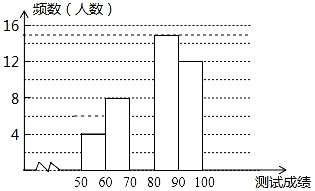

(1)、将频数分布直方图补充完整；

(2)、请求出所有参赛学生成绩的中位数落在哪个组内？

(3)、现将从包括小芳和小文在内的4名成绩优异的同学中随机选取两名参加市级比赛，求小芳与小文同时被选中的概率．

查看试题解析
21. 如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D ，过点D作DE⊥AC ，分别交AC、AB的延长线于点E ， F ．

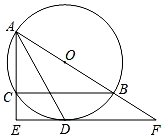(1)、求证：EF是⊙O的切线；

(2)、若AC＝6，CE＝2，求CB的长．

查看试题解析
22. 长沙市正在举行文化艺术节活动，一商店抓住商机，决定购进甲，乙两种艺术节纪念品．若购进甲种纪念品2件，乙种纪念品3件，需要400元；若购进甲种纪念品3件，乙种纪念品5件，需要650元．

(1)、求购进甲、乙两种纪念品每件各需多少元？

(2)、若该商店决定购进这两种纪念品共70件，其中乙种纪念品的数量不少于40件，考虑到资金周转，用于购买这70件纪念品的资金不能超过5750元，那么该商店共有几种进货方案？

查看试题解析
23. 已知正方形ABCD中AC与BD交于点O ，点M在线段BD上，作直线AM交直线DC于点E ，过D作DH⊥AE于H ，设直线DH交AC于点N ．

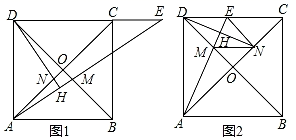(1)、如图1，当M在线段BO上时，求证：OM＝ON；

(2)、如图2，当M在线段OD上，连接NE和MN ，当EN $//$ BD时，求证：四边形DENM是菱形；

(3)、在（2）的条件下，若正方形边长为4，求EC的长．

查看试题解析
24. 我们不妨将函数图象关于y轴对称的函数称为“对称函数”．

(1)、判断下列函数是否为“对称函数”？
①y＝﹣2x；②y＝3x²+2；③y＝|x|．

(2)、已知对称函数y＝x²﹣2|x|﹣3．
①设函数位于y轴左侧图象与x轴的交点为A ， y轴右侧图象的最低点为B ，在y轴上找一点P ，使|PA﹣PB|值最大，求P点坐标．

②一次函数y＝x+b与y＝x²﹣2|x|﹣3有两个交点，求b的取值范围．

查看试题解析
25. 已知：二次函数y＝ $\frac{1}{2} x^{2}$ +2x+m的图象与x轴有公共点．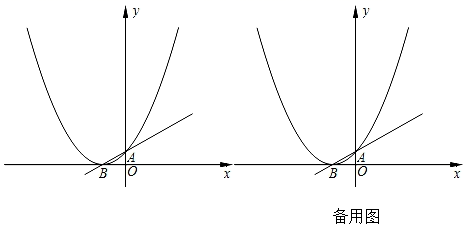

(1)、求m的取值范围；

(2)、如图所示，若二次函数y＝ $\frac{1}{2} x^{2}$ +2x+m图象的顶点B在x轴上，与y轴的交点为A ， P为图象上的一点，若以线段PB为直径的圆与直线AB相切于点B ，求P点的坐标；

(3)、在（2）中，若点P关于y轴的对称点为M ，求以点M为圆心，BP长为半径的圆是否与直线AB相切？并说明理由．

查看试题解析