湖南省张家界市永定区2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2020-12-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列函数是反比例函数的是（）

A、 $y = \frac{k}{x}$ B、 $y = \frac{2 x}{3}$ C、 $y = 2 x^{- 1}$ D、y=-x+5

查看试题解析
2. 反比例函数y= $\frac{4}{x}$ 的图象经过的象限是（）

A、第一二象限 B、第一三象限 C、第二三象限 D、第二四象限

查看试题解析
3. 下列四条线段能成比例线段的是（）

A、1，1，2，3 B、1，2，3，4 C、2，2，3，3 D、2，3，4，5

查看试题解析
4. 若 $(a - 2) x^{a^{2} - 2} = 3$ 是关于x的一元二次方程，则a的值是（）

A、4 B、2 C、－2 D、±2

查看试题解析
5. 如图，点 $D$ 、 $E$ 分别在 $△ A B C$ 的边 $A B$ 、 $A C$ 上，且 $D E$ 与 $B C$ 不平行．下列条件中，能判定 $△ A D E$ 与 $△ A C B$ 相似的是（　　）

A、 $\frac{A D}{A C} = \frac{A E}{A B}$ B、 $\frac{A D}{A E} = \frac{A B}{A C}$ C、 $\frac{D E}{B C} = \frac{A E}{A B}$ D、 $\frac{D E}{B C} = \frac{A D}{A C}$

查看试题解析
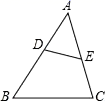6. 一元二次方程 $4 x^{2} = 12 x - 9$ 的根的情况是（）

A、只有一个实数根 B、没有实数根 C、有两个不相等的实数根 D、有两个相等的实数根

查看试题解析
7. 《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前，其中有首歌谣：今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？意即：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺，同时立一根一尺五寸的小标杆，它的影长五寸（提示：1丈=10尺，1尺=10寸），则竹竿的长为（）

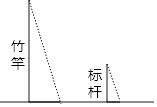A、五丈 B、四丈五尺 C、一丈 D、五尺

查看试题解析
8. 如图，在平行四边形ABCD中，点E在边DC上，DE：EC=5：2，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（）

A、5：7 B、10：4 C、25：4 D、25：49

查看试题解析

二、填空题

9. 若反比例函数的图象经过点（3，－1），则该反比例函数的表达式为．

查看试题解析
10. 如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC．已知AE=6， $\frac{A D}{D B} = \frac{3}{4}$ ，则EC的长等于．

查看试题解析
11. 一元二次方程 $x (x - 2) = x - 2$ 的根是.

查看试题解析
12. 若 $\frac{x}{x + y} = \frac{2}{5}$ ，则 $\frac{x}{y}$ =

查看试题解析
13. 若x=－2是方程x²+px+2q=0的根，则p－q的值是．

查看试题解析
14. 如图，平面直角坐标系中，等腰 $R t Δ A B C$ 的顶点 $A . B$ 分别在 $x$ 轴、 $y$ 轴的正半轴， $∠ A B C = 90^{\circ} ，$ $C A ⊥ x$ 轴，点 $C$ 在函数 $y = \frac{k}{x} (x > 0)$ 的图象上.若 $A B = 2 ，$ 则 $k$ 的值为.

查看试题解析

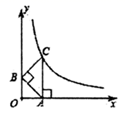
三、解答题

15. 用适当的方法解方程： $5 x^{2} - 4 x - 1 = 0$

查看试题解析
16. 已知y是x的反比例函数，并且当x=2时，y=4，

(1)、求y关于x的函数解析式；

(2)、当x=6时，求y的值．

查看试题解析
17. 如图，矩形ABCD中，E为BC上一点，连接AE，过顶点D作DF⊥AE，垂足为F，求证：△ABE∽△DFA．

查看试题解析
18. 阅读材料：设一元二次方程ax²+bx+c＝0(a≠0)的两根为x₁ ， x₂ ，则两根与方程系数之间有如下关系： $x_{1} + x_{2} = - \frac{b}{a}$ ，x₁·x₂＝ $\frac{c}{a}$ ．根据该材料解题：已知x₁ ， x₂是方程x²−2x=1的两实数根．
求：

(1)、 $x_{1}^{2} + x_{2}^{2}$

(2)、 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}}$

查看试题解析
19. 如图，在一个长10cm，宽6cm的矩形铁皮的四角各截去一个同样的小正方形，然后折叠成一个无盖的长方形盒子．若长方形盒子的底面（图中阴影部分）面积是32cm² ，求截去的小正方形的边长．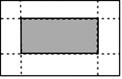

查看试题解析
20. 如图，已知A（−4，2），B（n，−4）是一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图像的两个交点．

(1)、求反比例函数和一次函数的解析式；

(2)、求直线AB与x轴的交点C的坐标及△AOB的面积；

(3)、求不等式 $k x + b - \frac{m}{x} > 0$ 的解集（请直接写出答案）．

查看试题解析
21. 关于x的一元二次方程x²－3x+k＝0有实数根．

(1)、求k的取值范围；

(2)、如果k是符合条件的最大整数，且一元二次方程 $(m - 1) x^{2} + x + m - 3 = 0$ 与方程 $x^{2} - 3 x + k = 0$ 有一个相同的根，求此时m的值．

查看试题解析
22. 在Rt△ABC中，∠C＝90°，AC＝8cm，BC＝6cm．现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿线段CB向点B方向运动．如果点P的速度是2cm/秒，点Q的速度是1cm/秒，它们同时出发，当有一点到达所在线段的端点时，就停止运动，设运动的时间为t秒．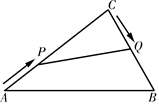

(1)、用含t的代数式表示Rt△CPQ的面积S；

(2)、当t＝2秒时，P，Q两点之间的距离是多少？

(3)、当t为多少秒时，以点C，P，Q为顶点的三角形与△ABC相似？

查看试题解析