四川省绵阳市三台县2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2020-12-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图标是节水、节能、低碳和绿色食品的标志，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，AD是 $△ A B C$ 的中线，已知 $△ A B D$ 的周长为25cm，AB比AC长6cm，则 $△ A C D$ 的周长为（）

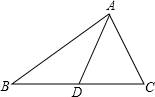A、19cm B、22cm C、25cm D、31cm

查看试题解析
3. 计算（a³）²正确的是（）

A、a B、a⁵ C、a⁶ D、a⁸

查看试题解析
4. 在平面直角坐标系中，点A(7，﹣2)关于x轴对称的点A'的坐标是（）

A、(7，2) B、(7，﹣2) C、(﹣7，2) D、(﹣7，﹣2)

查看试题解析
5. 下列计算中错误的是（）

A、a²•a⁴=a⁶ B、a⁶÷a³=a³ C、（ab）³=a³b³ D、（m³n－3m²n+ m²） ÷m²＝mn－3n

查看试题解析
6. 在△ABC和△A′B′C′中，AB= A′B′，∠B=∠B′，补充条件后仍不一定保证△ABC≌△A′B′C′，则补充的这个条件是（）

A、BC= B′C′ B、AC= A′C′ C、∠A=∠A′ D、∠C=∠C′

查看试题解析
7. 已知有理数x，y满足 $| x - 4 |$ + $\sqrt{y - 8}$ =0，则以x，y的值为两边长的等腰三角形的周长是（）

A、20或16 B、20 C、16 D、以上都不对

查看试题解析
8. 已知等腰三角形的一个外角等于100°，则它的顶角是( )

A、80° B、20° C、80°或20° D、不能确定

查看试题解析
9. 如图，正方形 $A B C D$ 的面积为 $16$ ， $△ A B E$ 是等边三角形，点 $E$ 在正方形 $A B C D$ 内，在对角线 $A C$ 上有一点 $P$ ，使 $P D + P E$ 的和最小，则这个最小值为（）．

A、 $\sqrt{8}$ B、 $3$ C、 $4$ D、 $\sqrt{32}$

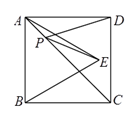查看试题解析
10. 如图，在△ABC中，PM、QN分别是AB、AC的垂直平分线，∠BAC＝100°那么∠PAQ等于（）

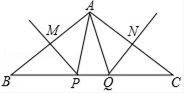A、50° B、40° C、30° D、20°

查看试题解析
11. 如图△BCD中，BE⊥CD，AE＝CE=3，BE＝DE=4．BC=5，DA的延长线交BC于F，则AF=（）

A、1 B、0.6 C、1.2 D、0.8

查看试题解析
12. 如图，C为线段BE上一动点 $（$ 不与点B，E重合 $）$ ，在BE同侧分别作等边ABC和等边CDE、BD与AE交于点P，BD与AC交于点M，AE与CD交于点N，连结MN．以下四个结论：①CM=CN；②∠APB=60°；③PA+PC=PB；④PC平分∠BPE；恒成立的结论有（）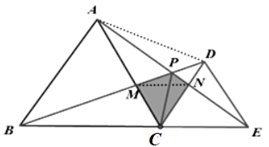

A、①②④ B、①②③④ C、①③④ D、①④

查看试题解析

二、填空题

13. （－ $\frac{4}{3}$ xy）·（－3xy）²=

查看试题解析
14. 已知 $a^{m} = 3$ ， $a^{n} = 5$ ，则 $a^{3 m + 2 n} =$

查看试题解析
15.
如图∠AOP=∠BOP=15°，PC∥OA ， PD⊥OA ，若PC=6，则PD等于.

查看试题解析
16. 如图，正五边形ABCDE，BG平分∠ABC，DG平分正五边形的外角∠EDF，则∠G＝度．

查看试题解析
17. 如图，△ABC中，AB=AC=12厘米，BC=9厘米，点D为AB的中点，如果点P在线段BC上以v厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动。若点Q的运动速度为3厘米/秒，则当△BPD与△CQP全等时，v的值为

查看试题解析
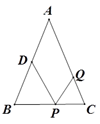18. 如图，在Rt直角△ABC中，∠B=45°，AB=AC，点D为BC中点，直角∠MDN绕点D旋转，DM，DN分别与边AB，AC交于E，F两点，下列结论：①△DEF是等腰直角三角形；②AE=CF；③△BDE≌△ADF；④BE+CF=EF，其中正确结论是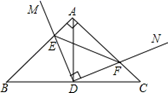

查看试题解析

三、解答题

19.

(1)、计算：－2²＋（π－3.14）⁰－ $| 1 - 2 \frac{1}{2} |$ ×（－2）；

(2)、化简求值：（x－3）（x－3）－（x＋2y）（x－2y）－4y² ，其中x＝－1

查看试题解析
20. 如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线MN交AC于点D，

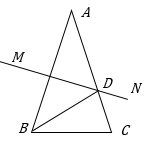(1)、求∠DBC的度数；

(2)、若BD=4，BC=6，求：△BDC的面积．

查看试题解析
21. △ABC在平面直角坐标系中的位置如图所示．

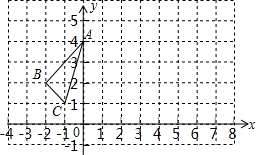(1)、作出△ABC关于y轴对称的△A₁B₁C₁ ，

(2)、将△ABC向右平移6个单位，作出平移后的△A₂B₂C₂ ，

(3)、观察△A₁B₁C₁和△A₂B₂C₂ ，它们是否关于某直线对称？若是，请写出对称轴，并在图上画出这条对称轴．

查看试题解析
22. $(x^{2} - m x + 6) (3 x - 2)$ 的积中不含x的二次项，求m的值．

查看试题解析
23. 如图，四边形ABCD中，点E在边CD上，连结AE、BE．已知：AD//BC；DE=CE；∠1=∠2；

求证：

(1)、∠3=∠4；

(2)、求证：AD+BC=AB．

查看试题解析
24. 如图，在平面直角坐标系中，点A的坐标为（2，0），以OA为边在第四象限做等边△AOB，点C为x轴正半轴一动点（OC > 2），连接BC，以BC为边在第四象限内作等边△CBD，直线DA交y轴于点E．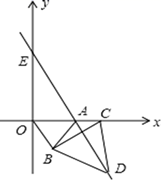

(1)、试问△OBC与△ABD全等吗？并证明你的结论；

(2)、随着点C位置的变化，∠AEO是否会发生变化？若没有变化，求出∠AEO的度数；若有变化，请说明理由．

(3)、若在x轴上有一动点P，使△PAE是等腰三角形，请直接写出满足条件的P点坐标．

查看试题解析