湖南省长沙市天心区长郡教育集团2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2020-12-14 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 在平面直角坐标系中点M（1，﹣2）在第（   ）象限.
    A、一 B、二 C、三 D、四

    查看试题解析

  • 2. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 3. 下面的调查方式中，你认为合适的是（   ）
    A、调查市场上酸奶的质量情况，采用抽样调查方式 B、了解长沙市居民日平均用水量，采用全面调查方式 C、乘坐飞机前的安检，采用抽样调查方式 D、某LED灯厂要检测一批灯管的使用寿命，采用全面调查方式

    查看试题解析

  • 4. 下列运算正确的是（   ）
    A、（m﹣n）（﹣m﹣n）＝﹣m2﹣n2 B、（﹣1+mn）（1+mn）＝﹣1﹣m2n2 C、（﹣m+n）（m﹣n）＝m2﹣n2 D、（2m﹣3）（2m+3）＝4m2﹣9

    查看试题解析

  • 5. 将点A（﹣2，3）通过以下哪种方式的平移，得到点A'（﹣5，7）（   ）
    A、沿x轴向右平移3个单位长度，再沿y轴向上平移4个单位长度 B、沿x轴向左平移3个单位长度，再沿y轴向下平移4个单位长度 C、沿x轴向左平移4个单位长度，再沿y轴向上平移3个单位长度 D、沿x轴向左平移3个单位长度，再沿y轴向上平移4个单位长度

    查看试题解析

  • 6. 下列运算正确的是（   ）
    A、a2•a3=a6 B、（a2）3=a5 C、（2a）2=4a2 D、3a2÷a2=3a

    查看试题解析

  • 7. 如图， △ABC 中， AB=AC ， D 是 BC 中点，下列结论中错误的是（    ）．

    A、∠B=∠C B、AD⊥BC C、AD 平分 ∠BAC D、AB=2BD

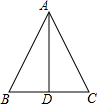    查看试题解析

  • 8. 我国古代数学名著《数书九章》有“米谷粒分”题：粮仓开仓收粮，有人送来米1500石，验得米内夹谷，抽样取米一把，数得300粒内夹谷30粒，则这批米内夹谷约为（   ）
    A、30石 B、150石 C、300石 D、50石

    查看试题解析

  • 9. 若(x+3)(x-5)=x2-mx-15，则m的值为（   ）
    A、2 B、-2 C、5 D、-5

    查看试题解析

  • 10. 如图，△ABC中，DE是AC的垂直平分线，AE= 5cm，△ABD的周长为16cm，则△ABC的周长为（   ）

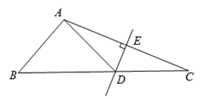    A、21cm B、26cm C、28cm D、31cm

    查看试题解析

  • 11. 已知x+y＝5，xy＝3，则x2+y2等于（    ）
    A、﹣19 B、19 C、﹣25 D、25

    查看试题解析

  • 12. 如图， ΔABC、ΔADE、ΔDFG 均为等边三角形， C、E、F 三点共线，且 E 是 CF 的中点，下列结论：① ΔADG≅ΔEDF ；② ΔAEC 为等腰三角形；③ DF=AD+GE ；④ ∠BAG=∠BCE ⑤ ∠GEB=60° ，其中正确的个数为（   ）

    A、2 B、3 C、4 D、5

    查看试题解析

二、填空题

  • 13. 等腰三角形的一个角是110°，则它的底角是 ．

    查看试题解析

  • 14. 计算：3a2b•（﹣2ab3）2= ．

    查看试题解析

  • 15. 如果点P（a﹣1，a+2）在x轴上，则a的值为 ．

    查看试题解析

  • 16. 定义一种新运算A※B＝A2+AB ． 例如（﹣2）※5＝（﹣2）2+（﹣2）×5＝﹣6．按照这种运算规定，（x+2）※（2﹣x）＝20，则x＝ ．

    查看试题解析

  • 17. 如图，∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=2， OB1=23 ，则△A1B1A2的面积是 ， △AnBnAn+1的面积是 ．

    查看试题解析

三、解答题

  • 18. 如图，△ABC中，AB＝6，AC＝7，BD、CD分别平分∠ABC、∠ACB，过点D作直线平行于BC，交AB、AC于E、F. 求△AEF的周长．

    查看试题解析

  • 19. 计算：
    (1)、x（4x2﹣x）+x3÷x；
    (2)、（x﹣y）（x+3y）﹣x（x+2y）．

    查看试题解析

  • 20. 先化简，再求值：（2+3x）（2﹣3x）+5x（x﹣1）+（2x﹣1）2 ， 其 x=−13 ．

    查看试题解析

  • 21.

    某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图．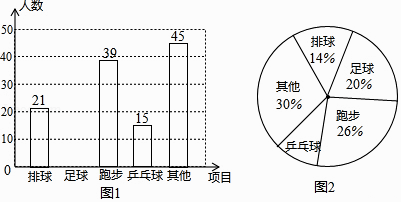

    请结合以上信息解答下列问题：

    (1)、m=；

    (2)、请补全上面的条形统计图；

    (3)、在图2中，“乒乓球”所对应扇形的圆心角的度数为；

    (4)、已知该校共有1200名学生，请你估计该校约有名学生最喜爱足球活动．

    查看试题解析

  • 22. 如图，△ABC的三个顶点在边长为1的正方形网格中，已知A（3，3），B（﹣3，﹣3），C（1，﹣3）．

    (1)、画出△ABC及关于y轴对称的△A1B1C1；
    (2)、写出点A的对应点A1的坐标是 ， 点B的对应点B1的坐标是 ， 点C的对应点C1的坐标是；
    (3)、请直接写出第四象限内以AB为边且与△ABC全等的三角形的第三个顶点（不与C重合）的坐标。

    查看试题解析

  • 23. 已知：△A1B1C1三个顶点的坐标分别为A1（﹣3，4），B1（﹣1，3），C1（1，6），把△A1B1C1先向右平移3个单位长度，再向下平移3个单位长度后得到△ABC ， 且点A1的对应点为A ， 点B1的对应点为B ， 点C1的对应点为C ．

    (1)、在坐标系中画出△ABC；
    (2)、求△ABC的面积；
    (3)、设点P在y轴上，且△APB与△ABC的面积相等，求点P的坐标．

    查看试题解析

  • 24. 如图，在 △ ABC中，AB＝AC ， 点D、E、F分别在AB、BC、AC边上，且BE＝CF ， CE＝DB ．

    (1)、求证： △ DEF是等腰三角形；
    (2)、当∠A＝50°时，求∠DEB+∠FEC的度数；
    (3)、当∠EDF＝60°时，求∠A的度数．

    查看试题解析

  • 25. 如图，在△ABC中．AB=AC ， 点E在线段BC上，连接AE并延长到G ， 使得EG=AE ， 过点G作GD∥BA分别交BC ， AC于点F ， D ．

    (1)、求证：△ABE≌△GFE；
    (2)、若GD=3，CD=1，求AB的长度；
    (3)、过点D作DH⊥BC于H ， P是直线DH上的一个动点，连接AF ， AP ， FP ， 若∠C=45°，在（2）的条件下，求△AFP周长的最小值．

    查看试题解析

  • 26. 如图，在平面直角坐标系中，点O为原点，△OAB为等边三角形，P、Q分别为AO、AB边上的动点，点P、点Q同时从点A出发，且当其中一点停止运动时，另一点也立即停止运动；若P以2个单位长度每秒的速度从点A向终点O运动，点Q以3个单位长度每秒的速度从点A向终点B运动，设运动时间为t ， 已知点A坐标为（a ， b），且满足（a﹣6）2+| 3 a﹣b|=0．

    (1)、求A点坐标；
    (2)、如图1，连接BP、OQ交于点C ， 请问当t为何值时，∠OCP=60°；
    (3)、如图2，D为OB边上的中点，P ， Q在运动过程中，D ， P ， Q三点是否能构成使∠PDQ=120°的等腰三角形，若能，求运动时间t并直接写出四边形APDQ的面积：若不能，请说明理由．

    查看试题解析