湖南省张家界市永定区2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2020-12-14 类型：期中考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值等于0，则x的值为（）

A、 $x = \pm 1$ B、x =1 C、 $x = - 1$ D、x = 0

查看试题解析
2. 下列命题中，属于真命题的是（）

A、相等的角是对顶角 B、一个角的补角大于这个角 C、绝对值最小的数是0 D、如果 $| a | = | b |$ ，那么a=b

查看试题解析
3. 下列分式中，是最简分式的是（）

A、 $\frac{x y}{x^{2}}$ B、 $\frac{2}{2 x - 2 y}$ C、 $\frac{x + y}{x^{2} - y^{2}}$ D、 $\frac{2 x}{x + 2}$

查看试题解析
4. 小芳有两根长度为6cm和10cm的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为（）的木条

A、2cm B、3cm C、8cm D、17cm

查看试题解析
5. 如图，点B，F，C，E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（）

A、AB=DE B、AC=DF C、BF=EC D、∠B=∠E

查看试题解析
6. 若把分式 $\frac{x + 3 y}{2 x y}$ 的x，y同时扩大2倍，则分式的值（）

A、扩大为原来的2倍 B、缩小为原来的 $\frac{1}{4}$ C、不变 D、缩小为原来的 $\frac{1}{2}$

查看试题解析
7. 如图， $△ A B C$ 中，DE是AC的垂直平分线，AE=4cm， $△ A B D$ 的周长为16cm，则 $△ A B C$ 的周长为（）

A、20cm B、24cm C、26cm D、36cm

查看试题解析
8. 已知 $x - \frac{1}{x} = 6$ ，则 $x^{2} + \frac{1}{x^{2}} - 6$ 的值是（）

A、28 B、30 C、32 D、34

查看试题解析

二、填空题

9. 全球芯片制造已经进入10纳米到7纳米器件的量产时代．中国自主研发的第一台7纳米刻蚀机，是芯片制造和微观加工最核心的设备之一，7纳米就是0.000000007米．数据0.000000007用科学记数法表示为．

查看试题解析
10. 如图，AD，CE是 $△ A B C$ 的两条高，已知AD=5，CE=4，AB=8，则BC的长是．

查看试题解析
11. 若 $2^{x} = 2, 4^{y} = 4$ ，则 $2^{x - 2 y}$ 的值为．

查看试题解析
12. 已知 $\frac{y}{x} = \frac{3}{2}$ ，则 $\frac{x - y}{x + y}$ = ．

查看试题解析
13. 当m＝时，分式方程 $\frac{x - 2}{x - 3} = \frac{m}{3 - x}$ 会出现增根

查看试题解析
14. “三等分角”大约是在公元前五世纪由古希腊人提出来的．借助如图所示的“三等分角仪”能三等分任何一个角．这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=78°，则∠AOB等于度．

查看试题解析

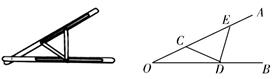
三、解答题

15. 计算：

(1)、 ${(- 2 x^{- 1} y^{3})}^{- 2}$

(2)、 $\frac{2}{y^{2} - 1} - \frac{2}{y + 1} - \frac{1}{y - 1}$

查看试题解析
16. 解方程： $\frac{2}{x - 1} + \frac{x + 2}{1 - x} = 3$

查看试题解析
17. 先化简，再求值： $\frac{x^{2}}{x - 1}$ ÷（1＋ $\frac{1}{x^{2} - 1}$ ），其中x＝2020．

查看试题解析
18. 如图，AB∥CD，AD和BC相交于点O，OB=OC．求证：OA=OD．

查看试题解析
19. 明陪妈妈一起到超市购买大米，按原价购买，用了100元．几天后，遇上这种大米8折出售，她用140元又买了一些，两次一共购买了55kg．这种大米的原价是多少？

查看试题解析
20. 如图，在△ABC中，AB＝AC，D是BC边上的中点，连结AD，BE平分∠ABC交AC于点E，过点E作EF∥BC交AB于点F．

(1)、若∠C＝38°，求∠BAD的度数；

(2)、求证：FB＝FE．

查看试题解析
21. 如图，△ABC是等边三角形，点D在AC上，以BD为一边作等边△BDE，连接CE．

(1)、说明△ABD ≌△CBE的理由；

(2)、若∠BEC＝82°，求∠DBC的度数．

查看试题解析
22.

(1)、探索：如果 $\frac{2 x + 3}{x - 1} = 2 + \frac{m}{x - 1}$ ，则m=；如果 $\frac{3 x - 1}{x + 1} = 3 + \frac{m}{x + 1}$ 则m=；

(2)、总结：如果 $\frac{a x + b}{x + c} = a + \frac{m}{x + c}$ （其中a，b，c为常数），则m=；（用含a，b，c的式子表示）；

(3)、利用上述结论解决：若代数式 $\frac{4 x - 3}{x - 1}$ 的值为整数，求满足条件的整数x的值．

查看试题解析