贵州省遵义市2020-2021学年高二上学期数学期中联合考试试卷
试卷更新日期:2020-12-14 类型:期中考试
一、单选题
-
1. 已知集合 , ,则 ( )A、{1} B、 C、 D、2. 已知向量 , ,若 ,则 ( )A、-1 B、0 C、 D、-23. 函数 的定义域为( )A、 B、 C、 D、4. 某中学开展劳动实习,组织学生加工制作零件.已知某零件的直观图如图1所示.某学生绘制出了该零件的正视图与俯视图如图2所示,则其侧视图为( )

 A、
A、 B、
B、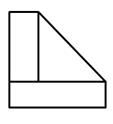 C、
C、 D、
D、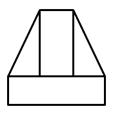 5. 已知 ,则 ( )A、 B、 C、 D、6. 下列函数中与函数 值域相同的是( )A、 B、 C、 D、7. 已知 为等差数列 的前 项和, , ,则 ( )A、 B、 C、 D、8. 函数 在区间 上的图象大致为( )A、
5. 已知 ,则 ( )A、 B、 C、 D、6. 下列函数中与函数 值域相同的是( )A、 B、 C、 D、7. 已知 为等差数列 的前 项和, , ,则 ( )A、 B、 C、 D、8. 函数 在区间 上的图象大致为( )A、 B、
B、 C、
C、 D、
D、 9. 图1是第七届国际数学教育大会( )的会徽图案,它是由一串直角三角形演化而成的(如图2),其中 ,则 ( )
9. 图1是第七届国际数学教育大会( )的会徽图案,它是由一串直角三角形演化而成的(如图2),其中 ,则 ( )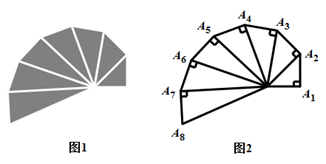 A、 B、 C、 D、10. 函数 的部分图象如图所示,则下列不正确的是( )
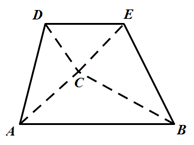
A、 B、 C、 D、10. 函数 的部分图象如图所示,则下列不正确的是( ) A、 B、 C、 D、11. 如图,在四面体 中,已知 , , ,则四面体 被截面 分得的上下两部分的体积之比为( )
A、 B、 C、 D、11. 如图,在四面体 中,已知 , , ,则四面体 被截面 分得的上下两部分的体积之比为( ) A、 B、 C、 D、12. 若一个圆柱的表面积为 ,则该圆柱的外接球的表面积的最小值为( )A、 B、 C、 D、
A、 B、 C、 D、12. 若一个圆柱的表面积为 ,则该圆柱的外接球的表面积的最小值为( )A、 B、 C、 D、二、填空题
-
13. 已知幂函数 的图象经过点 ,则 .14. 设 , 满足约束条件 ,则 的最大值是.15. 已知 是面积为 的等边三角形,点 在线段 的延长线上,若 ,则 .16. 已知函数 在 上的最大值为 ,最小值为 ,则 .
三、解答题
-
17. 长方体 的底面 是边长为1的正方形,其外接球的表面积为 .
 (1)、求该长方体的表面积;(2)、求异面直线 与 所成角的余弦值.18. 已知 是各项均为正数的等比数列, 为 , 的等差中项.(1)、求 的公比;(2)、若 ,设 ,求数列 的前 项和.19. 已知函数 满足 .(1)、求 的解析式;(2)、若 的定义域为 ,求函数 的值域.
(1)、求该长方体的表面积;(2)、求异面直线 与 所成角的余弦值.18. 已知 是各项均为正数的等比数列, 为 , 的等差中项.(1)、求 的公比;(2)、若 ,设 ,求数列 的前 项和.19. 已知函数 满足 .(1)、求 的解析式;(2)、若 的定义域为 ,求函数 的值域.