河南省2020-2021学年高一上学期数学期中考试试卷
试卷更新日期:2020-12-11 类型:期中考试
一、单选题
-
1. 已知集合A={x||x|≤3,x∈Z},B={x|-1<x<5},则A∩B中元素的个数为( )A、3 B、4 C、5 D、62. 下列函数中,为偶函数的是( )A、 B、y=2x C、y=x2-2x+1 D、y=|x|3. 已知函数 ,则f(f(4))=( )A、-2 B、0 C、4 D、164. 函数f(x)= 的定义域为( )A、 B、 C、 D、5. 函数f(x)= 的图象大致为( )A、
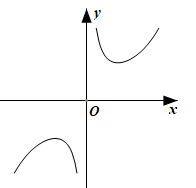 B、
B、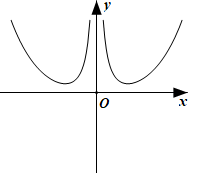 C、
C、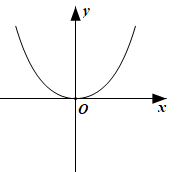 D、
D、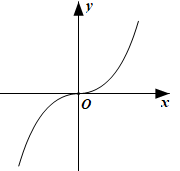 6. 函数f(x)=lgx- (x∈(1,10))的值域为( )A、(0,1) B、(-1,1) C、(-1, ) D、(0, )7. 已知 是定义在 上的奇函数且单调递增, ,则 的取值范围是( )A、 B、 C、 D、8. 设 ,则( )A、c>b>a B、c>a>b C、b>a>c D、a>b>c9. 已知幂函数f(x)= (k∈N*),则使得f(x)为奇函数,且在(0,+∞)上单调递增的k的个数为( )A、0 B、1 C、2 D、无数个10. 已知函数f(x)= ,在(0,a-5)上单调递减,则实数a的取值范围是( )A、[6,8] B、[6,7] C、(5,8] D、(5,7]11. 已知函数f(x)=|log2(x-1)|,若x1≠x2 , f(x1)=f(x2),则 ( )A、 B、1 C、2 D、12. 若3a-3b>2b-2a , 则下列不等式正确的是( )
6. 函数f(x)=lgx- (x∈(1,10))的值域为( )A、(0,1) B、(-1,1) C、(-1, ) D、(0, )7. 已知 是定义在 上的奇函数且单调递增, ,则 的取值范围是( )A、 B、 C、 D、8. 设 ,则( )A、c>b>a B、c>a>b C、b>a>c D、a>b>c9. 已知幂函数f(x)= (k∈N*),则使得f(x)为奇函数,且在(0,+∞)上单调递增的k的个数为( )A、0 B、1 C、2 D、无数个10. 已知函数f(x)= ,在(0,a-5)上单调递减,则实数a的取值范围是( )A、[6,8] B、[6,7] C、(5,8] D、(5,7]11. 已知函数f(x)=|log2(x-1)|,若x1≠x2 , f(x1)=f(x2),则 ( )A、 B、1 C、2 D、12. 若3a-3b>2b-2a , 则下列不等式正确的是( )①ln(a-b+1)>0;②ln(b-a+1)>0;③ea-b-1>0;④eb-a-1>0
A、①③ B、①④ C、②③ D、②④二、填空题
-
13. 已知幂函数y=xα的图象过点(4, ),则α=.14. 已知log2a=log43+log169,则a=.15. 函数f(x)= 的最大值为.16. 某汽车厂商生产销售一款电动汽车,每辆车的成本为4万元,销售价格为6万元,平均每月销量为800辆,今年该厂商对这款汽车进行升级换代,成本维持不变,但为了提高利润,准备提高销售价格,经过市场分析后发现,如果每辆车价格上涨0.1万元,月销量就会减少20辆,为了获取最大利润,每辆车的销售价格应定为万元.
三、解答题
-
17. 化简求值:(1)、 ;(2)、log6(log264)+ .18. 已知集合A={y|y=ex , x>0},B={x|y= }.(1)、求A∩( B);(2)、设集合M={x|a<x≤3-a},若M B,求实数a的取值范围.19. 已知函数 .(1)、判断 的单调性并用定义证明;(2)、若对任意的 恒成立,求实数m的取值范围.20. 已知函数 , .(1)、当 分别为奇函数和偶函数时,求 的值;(2)、若 为奇函数,证明:对任意的 、 , .21. 锂电池的容量通常以A·h(安培小时)为单位,在一定条件下,当以恒定电流充电时把电池充满所需要的充电时间t(单位:h)等于电池的容量与充电电流x(单位:A)之比.电池充电时会产生额外的能量损失(不影响电池充入的电量).已知某种锂电池的容量为20A·h,且充电时每小时的能量损失P(能量单位)与充电电流x的关系式为P= .设这种锂电池的电量从0到充满电的能量损失总量为Q.(1)、若 ,求充电电流x的取值范围;(2)、充电电流为多大时,Q的值最小?最小值为多少?
参考结论:函数y=ax+ (a,b>0)在区间(0, )上单调递减,在区间( ,+∞)上单调递增.
22. 设 ,已知函数 , .(1)、求a的值;(2)、求函数f(x)的最小值;(3)、若方程f(x)-m=0在区间(1,4)上有两个不相等的实根,求实数m的取值范围.