山东省烟台市2021年高三上学期数学期中考试试卷
试卷更新日期:2020-12-11 类型:期中考试
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 若非零向量 的夹角为 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 若 ,则 ( )A、 B、 C、 D、4. 设 ,则 的大小关系为( )A、 B、 C、 D、5. 若M为 的边AB上一点,且 则 ( )A、 B、 C、 D、6. 函数 在其定义域上的图象大致为( )A、
 B、
B、 C、
C、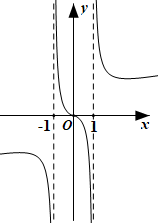 D、
D、 7. 牛顿冷却定律描述一个物体在常温环境下的温度变化:如果物体的初始温度为 ,则经过一定时间 后的温度T将满足 ,其中 是环境温度,h称为半衰期.现有一杯85℃的热茶,放置在25℃的房间中,如果热茶降温到55℃,需要10分钟,则欲降温到45℃,大约需要多少分钟?( )(1g2≈0.3010,1g3≈0.4771)A、12 B、14 C、16 D、188. 已知函数 ,若函数 有两个不同的零点,则实数 的取值范围是( )A、 B、 C、 D、
7. 牛顿冷却定律描述一个物体在常温环境下的温度变化:如果物体的初始温度为 ,则经过一定时间 后的温度T将满足 ,其中 是环境温度,h称为半衰期.现有一杯85℃的热茶,放置在25℃的房间中,如果热茶降温到55℃,需要10分钟,则欲降温到45℃,大约需要多少分钟?( )(1g2≈0.3010,1g3≈0.4771)A、12 B、14 C、16 D、188. 已知函数 ,若函数 有两个不同的零点,则实数 的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 若 ,则( )A、 B、 C、 D、10. 已知 是定义在R上的奇函数,且满足 ,则下列说法正确的是( )A、 B、 在区间 上单调递增 C、 D、 是满足条件的一个函数11. 函数 ,( 是常数, )的部分图象如图所示,则( )
 A、 B、 C、 的对称轴为 D、 的递减区间为12. 已知函数 , ,则下列结论正确的有( )A、 在区间 上单调递减 B、若 ,则 C、 在区间 上的值域为 D、若函数 ,且 , 在 上单调递减
A、 B、 C、 的对称轴为 D、 的递减区间为12. 已知函数 , ,则下列结论正确的有( )A、 在区间 上单调递减 B、若 ,则 C、 在区间 上的值域为 D、若函数 ,且 , 在 上单调递减三、填空题
-
13. 设 为单位向量,且 ,则14. 函数 的定义域为15. 已知函数 是定义在R上的偶函数,其导函数为 ,若对任意的正实数, ,则不等式 的解集为16. 如图,C、D是两所学校所在地,C、D到一条公路的垂直距离分别为 .为了缓解上下学的交通压力,决定在AB上找一点P,分别向C、D修建两条互相垂直的公路PC和PD,设 ,则当 最小时, .

四、解答题
-
17. 在平面直角坐标系 中,已知向量 .(1)、若 ,求 的值;(2)、若 在 上的投影向量长度为 ,求 的值.18. 某市作为新兴的“网红城市”,有很多风靡网络的“网红景点”,每年都有大量的游客来参观旅游。为提高经济效益,管理部门对某一景点进行了改造升级,经市场调查,改造后旅游增加值y万元投入 万元之间满足: (a,b为常数),当 万元时, 万元;当 万元时, 万元.(参考数据: )(1)、写出该景点改造升级后旅游增加利润 万元与投入 万元的函数解析式;(利润=旅游增加值-投入)(2)、投入多少万元时,旅游增加利润最大?最大利润是多少万元?(精确到0.1)19. 在① ,② ,③ 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求 的值;若问题中的三角形不存在,说明理由.
问题:在 中,它的内角A,B,C的对边分别为 ,若 的外接圆半径为2,且 ,___________.
注:如果选择多个条件分别解答,按第一个解答计分.