2017年台湾省中考数学试卷
试卷更新日期:2017-10-10 类型:中考真卷
一、选择题
-
1. 算式(﹣2)×|﹣5|﹣|﹣3|之值为何( )A、13 B、7 C、﹣13 D、﹣72. 下列哪一个选项中的等式成立( )A、 =2 B、 =3 C、 =4 D、 =53. 计算6x•(3﹣2x)的结果,与下列哪一个式子相同( )A、﹣12x2+18x B、﹣12x2+3 C、16x D、6x4. 若阿光以四种不同的方式连接正六边形ABCDEF的两条对角线,连接后的情形如下列选项中的图形所示,则下列哪一个图形不是轴对称图形( )A、
 B、
B、 C、
C、 D、
D、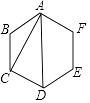 5. 已知坐标平面上有两直线相交于一点(2,a),且两直线的方程式分别为2x+3y=7,3x﹣2y=b,其中a,b为两数,求a+b之值为何( )
5. 已知坐标平面上有两直线相交于一点(2,a),且两直线的方程式分别为2x+3y=7,3x﹣2y=b,其中a,b为两数,求a+b之值为何( )
A、1 B、﹣1 C、5 D、﹣56. 阿信、小怡两人打算搭乘同一班次电车上学,若此班次电车共有5节车厢,且阿信从任意一节车厢上车的机会相等,小怡从任意一节车厢上车的机会相等,则两人从同一节车厢上车的概率为何( )A、 B、 C、 D、7. 平面上有A,B,C三点,其中AB=3,BC=4,AC=5,若分别以A,B,C为圆心,半径长为2画圆,画出圆A,圆B,圆C,则下列叙述何者正确( )A、圆A与圆C外切,圆B与圆C外切 B、圆A与圆C外切,圆B与圆C外离 C、圆A与圆C外离,圆B与圆C外切 D、圆A与圆C外离,圆B与圆C外离8. 下列选项中所表示的数,哪一个与252的最大公因数为42( )A、2×3×52×72 B、2×32×5×72 C、22×3×52×7 D、22×32×5×79. 某高中的篮球队球员中,一、二年级的成员共有8人,三年级的成员有3人,一、二年级的成员身高(单位:公分)如下:172,172,174,174,176,176,178,178
若队中所有成员的平均身高为178公分,则队中三年级成员的平均身高为几公分( )
A、178 B、181 C、183 D、18610. 已知在卡乐芙超市内购物总金额超过190元时,购物总金额有打八折的优惠,安妮带200元到卡乐芙超市买棒棒糖.若棒棒糖每根9元,则她最多可买多少根棒棒糖( )A、22 B、23 C、27 D、2811. 如图,△ABC中,D,E两点分别在AB,BC上,若AD:DB=CE:EB=2:3,则△DBE与△ADC的面积比为( ) A、3:5 B、4:5 C、9:10 D、15:1612. 一元二次方程式x2﹣8x=48可表示成(x﹣a)2=48+b的形式,其中a、b为整数,求a+b之值为何( )A、20 B、12 C、﹣12 D、﹣2013. 已知坐标平面上有一长方形ABCD,其坐标分别为A(0,0),B(2,0),C(2,1),D(0,1),今固定B点并将此长方形依顺时针方向旋转,如图所示.若旋转后C点的坐标为(3,0),则旋转后D点的坐标为何( )
A、3:5 B、4:5 C、9:10 D、15:1612. 一元二次方程式x2﹣8x=48可表示成(x﹣a)2=48+b的形式,其中a、b为整数,求a+b之值为何( )A、20 B、12 C、﹣12 D、﹣2013. 已知坐标平面上有一长方形ABCD,其坐标分别为A(0,0),B(2,0),C(2,1),D(0,1),今固定B点并将此长方形依顺时针方向旋转,如图所示.若旋转后C点的坐标为(3,0),则旋转后D点的坐标为何( ) A、(2,2) B、(2,3) C、(3,3) D、(3,2)14. 如图为平面上五条直线L1 , L2 , L3 , L4 , L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )
A、(2,2) B、(2,3) C、(3,3) D、(3,2)14. 如图为平面上五条直线L1 , L2 , L3 , L4 , L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )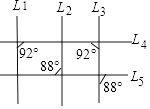 A、L1和L3平行,L2和L3平行 B、L1和L3平行,L2和L3不平行 C、L1和L3不平行,L2和L3平行 D、L1和L3不平行,L2和L3不平行15. 威立到小吃店买水饺,他身上带的钱恰好等于15粒虾仁水饺或20粒韭菜水饺的价钱,若威立先买了9粒虾仁水饺,则他身上剩下的钱恰好可买多少粒韭菜水饺( )A、6 B、8 C、9 D、1216. 将图1中五边形纸片ABCDE的A点以BE为折线往下折,A点恰好落在CD上,如图2所示,再分别以图2的AB,AE为折线,将C,D两点往上折,使得A,B,C,D,E五点均在同一平面上,如图3所示,若图1中∠A=124°,则图3中∠CAD的度数为何( )
A、L1和L3平行,L2和L3平行 B、L1和L3平行,L2和L3不平行 C、L1和L3不平行,L2和L3平行 D、L1和L3不平行,L2和L3不平行15. 威立到小吃店买水饺,他身上带的钱恰好等于15粒虾仁水饺或20粒韭菜水饺的价钱,若威立先买了9粒虾仁水饺,则他身上剩下的钱恰好可买多少粒韭菜水饺( )A、6 B、8 C、9 D、1216. 将图1中五边形纸片ABCDE的A点以BE为折线往下折,A点恰好落在CD上,如图2所示,再分别以图2的AB,AE为折线,将C,D两点往上折,使得A,B,C,D,E五点均在同一平面上,如图3所示,若图1中∠A=124°,则图3中∠CAD的度数为何( ) A、56 B、60 C、62 D、6817. 若a,b为两质数且相差2,则ab+1之值可能为下列何者( )A、392 B、402 C、412 D、42218. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
A、56 B、60 C、62 D、6817. 若a,b为两质数且相差2,则ab+1之值可能为下列何者( )A、392 B、402 C、412 D、42218. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( ) A、O是△AEB的外心,O是△AED的外心 B、O是△AEB的外心,O不是△AED的外心 C、O不是△AEB的外心,O是△AED的外心 D、O不是△AEB的外心,O不是△AED的外心19. 如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )
A、O是△AEB的外心,O是△AED的外心 B、O是△AEB的外心,O不是△AED的外心 C、O不是△AEB的外心,O是△AED的外心 D、O不是△AEB的外心,O不是△AED的外心19. 如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( ) A、∠1=∠2>∠3 B、∠1=∠3>∠2 C、∠2>∠1=∠3 D、∠3>∠1=∠220. 如图的数轴上有O,A,B三点,其中O为原点,A点所表示的数为106 , 根据图中数轴上这三点之间的实际距离进行估计,下列何者最接近B点所表示的数( )
A、∠1=∠2>∠3 B、∠1=∠3>∠2 C、∠2>∠1=∠3 D、∠3>∠1=∠220. 如图的数轴上有O,A,B三点,其中O为原点,A点所表示的数为106 , 根据图中数轴上这三点之间的实际距离进行估计,下列何者最接近B点所表示的数( )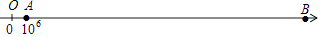 A、2×106 B、4×106 C、2×107 D、4×10821. 如图,△ABC、△ADE中,C、E两点分别在AD,AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )
A、2×106 B、4×106 C、2×107 D、4×10821. 如图,△ABC、△ADE中,C、E两点分别在AD,AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )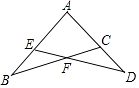 A、2 B、2 C、2+ D、2+22. 已知坐标平面上有两个二次函数y=a(x+1)(x﹣7),y=b(x+1)(x﹣15)的图形,其中a、b为整数.判断将二次函数y=b(x+1)(x﹣15)的图形依下列哪一种方式平移后,会使得此两图形的对称轴重叠( )A、向左平移4单位 B、向右平移4单位 C、向左平移8单位 D、向右平移8单位23. 如图为阿辉,小燕一起到商店分别买了数杯饮料与在家分饮料的经过.
A、2 B、2 C、2+ D、2+22. 已知坐标平面上有两个二次函数y=a(x+1)(x﹣7),y=b(x+1)(x﹣15)的图形,其中a、b为整数.判断将二次函数y=b(x+1)(x﹣15)的图形依下列哪一种方式平移后,会使得此两图形的对称轴重叠( )A、向左平移4单位 B、向右平移4单位 C、向左平移8单位 D、向右平移8单位23. 如图为阿辉,小燕一起到商店分别买了数杯饮料与在家分饮料的经过.
若每杯饮料的价格均相同,则根据图中的对话,判断阿辉买了多少杯饮料( )
A、22 B、25 C、47 D、5024. 如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( ) A、43 B、44 C、45 D、4625. 如图,某计算机中有
A、43 B、44 C、45 D、4625. 如图,某计算机中有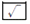 、
、  、
、  三个按键,以下是这三个按键的功能.
三个按键,以下是这三个按键的功能.①
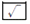 :将荧幕显示的数变成它的正平方根,例如:荧幕显示的数为49时,按下
:将荧幕显示的数变成它的正平方根,例如:荧幕显示的数为49时,按下  后会变成7.
后会变成7.②
 :将荧幕显示的数变成它的倒数,例如:荧幕显示的数为25时,按下
:将荧幕显示的数变成它的倒数,例如:荧幕显示的数为25时,按下  后会变成0.04.
后会变成0.04.③
 :将荧幕显示的数变成它的平方,例如:荧幕显示的数为6时,按下
:将荧幕显示的数变成它的平方,例如:荧幕显示的数为6时,按下  后会变成36.
后会变成36.若荧幕显示的数为100时,小刘第一下按
 ,第二下按
,第二下按  ,第三下按
,第三下按  ,之后以
,之后以  、
、  、
、  的顺序轮流按,则当他按了第100下后荧幕显示的数是多少( )
的顺序轮流按,则当他按了第100下后荧幕显示的数是多少( ) A、0.01 B、0.1 C、10 D、10026. 如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD,BPQR的面积分别为16、25,则四边形RBCS的面积为何( )
A、0.01 B、0.1 C、10 D、10026. 如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD,BPQR的面积分别为16、25,则四边形RBCS的面积为何( ) A、8 B、 C、 D、
A、8 B、 C、 D、二、解答题
-
27. 今有甲、乙、丙三名候选人参与某村村长选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人之得票数内,全村设有四个投开票所,目前第一、第二、第三投开票所已开完所有选票,剩下第四投开票所尚未开票,结果如表所示:
投开票所
候选人
废票
合计
甲
乙
丙
一
200
211
147
12
570
二
286
85
244
15
630
三
97
41
205
7
350
四
250
(单位:票)
请回答下列问题:
(1)、请分别写出目前甲、乙、丙三名候选人的得票数;(2)、承(1),请分别判断甲、乙两名候选人是否还有机会当选村长,并详细解释或完整写出你的解题过程.28. 如图,在坐标平面上,O为原点,另有A(0,3),B(﹣5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题: (1)、已知直线L的方程为5x﹣3y=k,求k的值.(2)、承(1),请完整说明△AOB与△COD相似的理由.
(1)、已知直线L的方程为5x﹣3y=k,求k的值.(2)、承(1),请完整说明△AOB与△COD相似的理由.