2017年四川省乐山市中考数学试卷
试卷更新日期:2017-10-10 类型:中考真卷
一、选择题:
-
1. ﹣2的倒数是( )A、﹣ B、 C、2 D、﹣22. 随着经济发展,人民的生活水平不断提高,旅游业快速增长,2016年国民出境旅游超过120 000 000人次,将120 000 000用科学记数法表示为( )A、1.2×109 B、12×107 C、0.12×109 D、1.2×1083. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、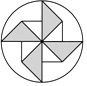 C、
C、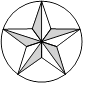 D、
D、 4. 含30°角的直角三角板与直线l1、l2的位置关系如图所示,已知l1∥l2 , ∠ACD=∠A,则∠1=( )
4. 含30°角的直角三角板与直线l1、l2的位置关系如图所示,已知l1∥l2 , ∠ACD=∠A,则∠1=( )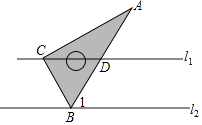 A、70° B、60° C、40° D、30°5. 下列说法正确的是( )A、打开电视,它正在播广告是必然事件 B、要考察一个班级中的学生对建立生物角的看法适合用抽样调查 C、在抽样调查过程中,样本容量越大,对总体的估计就越准确 D、甲、乙两人射中环数的方差分别为S甲2=2,S乙2=4,说明乙的射击成绩比甲稳定6. 若a2﹣ab=0(b≠0),则 =( )A、0 B、 C、0或 D、1或 27. 如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
A、70° B、60° C、40° D、30°5. 下列说法正确的是( )A、打开电视,它正在播广告是必然事件 B、要考察一个班级中的学生对建立生物角的看法适合用抽样调查 C、在抽样调查过程中,样本容量越大,对总体的估计就越准确 D、甲、乙两人射中环数的方差分别为S甲2=2,S乙2=4,说明乙的射击成绩比甲稳定6. 若a2﹣ab=0(b≠0),则 =( )A、0 B、 C、0或 D、1或 27. 如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( ) A、2米 B、2.5米 C、2.4米 D、2.1米8. 已知x+ =3,则下列三个等式:①x2+ =7,②x﹣ ,③2x2﹣6x=﹣2中,正确的个数有( )A、0个 B、1个 C、2个 D、3个9. 已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是( )A、 B、 C、 或 D、 或10. 如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y= 的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
A、2米 B、2.5米 C、2.4米 D、2.1米8. 已知x+ =3,则下列三个等式:①x2+ =7,②x﹣ ,③2x2﹣6x=﹣2中,正确的个数有( )A、0个 B、1个 C、2个 D、3个9. 已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是( )A、 B、 C、 或 D、 或10. 如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y= 的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )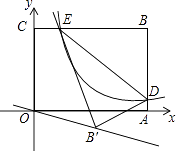 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:
-
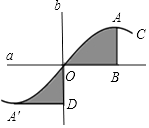
11. 3﹣2= .12. 二元一次方程组 = =x+2的解是 .13. 如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 .
 14. 点A,B,C在格点图中的位置如图5所示,格点小正方形的边长为1,则点C到线段AB所在直线的距离是 .
14. 点A,B,C在格点图中的位置如图5所示,格点小正方形的边长为1,则点C到线段AB所在直线的距离是 . 15. 庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1= + + +…+ +….
15. 庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1= + + +…+ +….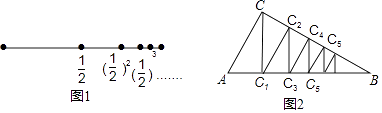
图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作CC1⊥AB于点C1 , 再过点C1作C1C2⊥BC于点C2 , 又过点C2作C2C3⊥AB于点C3 , 如此无限继续下去,则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、….假设AC=2,这些三角形的面积和可以得到一个等式是 .
16. 对于函数y=xn+xm , 我们定义y'=nxn﹣1+mxm﹣1(m、n为常数).例如y=x4+x2 , 则y'=4x3+2x.
已知:y= x3+(m﹣1)x2+m2x.
(1)、若方程y′=0有两个相等实数根,则m的值为;(2)、若方程y′=m﹣ 有两个正数根,则m的取值范围为 .三、综合题
-
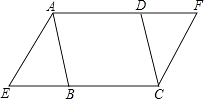
17. 计算:2sin60°+|1﹣ |+20170﹣ .18. 求不等式组 的所有整数解.19. 如图,延长▱ABCD的边AD到F,使DF=DC,延长CB到点E,使BE=BA,分别连结点A,E和C,F.求证:AE=CF.
 20. 化简:( ﹣ )÷ .21. 为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:
20. 化简:( ﹣ )÷ .21. 为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:组别
分数段(分)
频数
频率
A组
60≤x<70
30
0.1
B组
70≤x<80
90
n
C组
80≤x<90
m
0.4
D组
90≤x<100
60
0.2
 (1)、在表中:m= , n=;(2)、补全频数分布直方图;(3)、小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在组;(4)、4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.22. 如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,求树高DE的长度.
(1)、在表中:m= , n=;(2)、补全频数分布直方图;(3)、小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在组;(4)、4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.22. 如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,求树高DE的长度.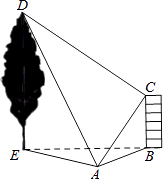 23. 某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
23. 某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:年 度
2013
2014
2015
2016
投入技改资金x(万元)
2.5
3
4
4.5
产品成本y(万元/件)
7.2
6
4.5
4
(1)、请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;(2)、按照这种变化规律,若2017年已投入资金5万元.①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
24. 如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.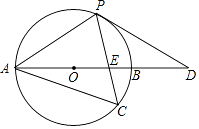 (1)、试判断PD与⊙O的位置关系,并说明理由;(2)、若点C是弧AB的中点,已知AB=4,求CE•CP的值.25. 在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.
(1)、试判断PD与⊙O的位置关系,并说明理由;(2)、若点C是弧AB的中点,已知AB=4,求CE•CP的值.25. 在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.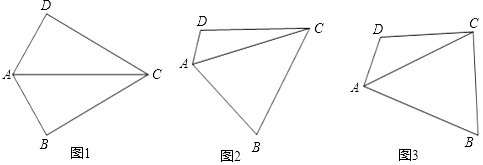 (1)、如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.(2)、如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.(3)、如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.26. 如图1,抛物线C1:y=x2+ax与C2:y=﹣x2+bx相交于点O、C,C1与C2分别交x轴于点B,A,且B为线段AO的中点.
(1)、如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.(2)、如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.(3)、如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.26. 如图1,抛物线C1:y=x2+ax与C2:y=﹣x2+bx相交于点O、C,C1与C2分别交x轴于点B,A,且B为线段AO的中点.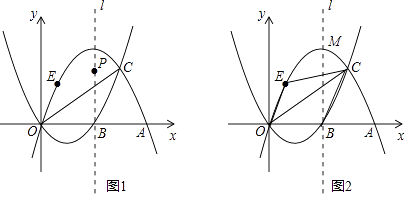 (1)、求 的值;(2)、若OC⊥AC,求△OAC的面积;(3)、抛物线C2的对称轴为l,顶点为M,在(2)的条件下:
(1)、求 的值;(2)、若OC⊥AC,求△OAC的面积;(3)、抛物线C2的对称轴为l,顶点为M,在(2)的条件下:①点P为抛物线C2对称轴l上一动点,当△PAC的周长最小时,求点P的坐标;
②如图2,点E在抛物线C2上点O与点M之间运动,四边形OBCE的面积是否存在最大值?若存在,求出面积的最大值和点E的坐标;若不存在,请说明理由.