初中数学苏科版七年级上学期期末复习专题5 代数式

试卷更新日期：2020-12-10 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列判断：① $- \frac{{xy}^{2}}{π}$ 不是单项式；② $\frac{x - y}{3}$ 是多项式；③0不是单项式；④ $\frac{1 + x}{x}$ 是整式.其中正确的有（）

A、2个 B、1个 C、3个 D、4个

查看试题解析
2. 若 $\frac{1}{3} x^{n + 5} y^{5}$ 和 $x^{4} y^{m + 2}$ 的差为单项式，则 $n^{2} + m n$ 值为（）

A、4 B、－4 C、－2 D、2

查看试题解析
3. 设 $A = x^{2} - 3 x - 2$ ， $B = 2 x^{2} - 3 x - 1$ ，若x取任意有理数，则A与B的大小关系为（）

A、 $A < B$ B、 $A = B$ C、 $A > B$ D、无法比较

查看试题解析
4. 已知a+b=7，ab=10，则代数式(5ab+4a+7b)+(3a–4ab)的值为（）

A、49 B、59 C、77 D、139

查看试题解析
5. 三角形的一条边长是 $a + b$ ，第二条边比第一条边长 $a + 2$ ，第三条边比第二条边短3，则这个三角形的周长为(　　)

A、 $5 a + 3 b$ B、 $5 a - 3 b + 1$ C、 $5 a + 3 b + 1$ D、 $5 a + 3 b - 1$

查看试题解析
6. 下列各项去括号正确的是（）

A、﹣3（m+n）﹣mn=﹣3m+3n﹣mn B、﹣（5x﹣3y）+4（2xy﹣y²）=﹣5x+3y+8xy﹣4y² C、ab﹣5（﹣a+3）=ab+5a﹣3 D、x²﹣2（2x﹣y+2）=x²﹣4x﹣2y+4

查看试题解析
7. 若某矿山2018年采矿量为n吨，经过技术改良后，预计2019年采矿量将比2018年增产30%，则2019年该矿山的预计采矿量是（）吨

A、（1-30%）n B、（1+30%）n C、n+30% D、30%n

查看试题解析
8. 设三个互不相等的有理数，既可表示为 1、 $a + b$ 、a 的形式，又可表示为 0、 $\frac{b}{a}$ 、b 的形式，则 $a^{2021} + b^{2021}$ 的值为（）

A、0 B、 $- 1$ C、1 D、2

查看试题解析
9. 在课题学习中，老师要求用长为12厘米，宽为8厘米的长方形纸片制作一个无盖的长方体纸盒．三位同学分别以下列方式在长方形纸片上截去两角（图中阴影部分），然后沿虚线折成一个无盖的长方体纸盒．
甲：如图1，盒子底面的四边形ABCD是正方形；

乙：如图2，盒子底面的四边形ABCD是正方形；

丙：如图3，盒子底面的四边形ABCD是长方形，AB=2AD．

将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列，正确的是

A、甲＞乙＞丙 B、甲＞丙＞乙 C、丙＞甲＞乙 D、丙＞乙＞甲

查看试题解析
10. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为mcm，宽为ncm)的盒子底部(如图②)盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（）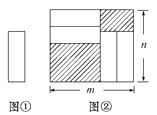

A、4mcm B、4ncm C、2(m+n)cm D、4(m-n)cm

查看试题解析

二、填空题

11. 如图是一个计算程序，若输入a的值为﹣2，则输出的结果应为．

查看试题解析
12. 已知一个三角形的三边长分别为 $(2 x + 1) c m$ ， $(x^{2} - 2) c m$ ， $(x^{2} - 2 x + 1) c m$ ，则该三角形的周长为cm.

查看试题解析
13. 多项式 $(a - 2) x^{5} - \frac{2}{3} x^{b} + x - 9$ 是关于x的四次三项式，则ab的值为.

查看试题解析
14. 当1<a<2时，代数式|a-2|+|1-a|的值是。

查看试题解析
15. 如果 $a x^{2} y + 2 b x^{3} y + 4 x^{2} y + c = 3 x^{2} y + 4 x^{3} y + 1$ 所以 $a + b + c =$ ．

查看试题解析
16. 已知x＝2019时，代数式ax³+bx﹣2的值是2，当x＝﹣2019时，代数式ax³+bx+5的值等于．

查看试题解析
17. 若式子2x²+ax-y+b-(2bx²-3x+5y-1)的值不含x²和x，则2a+b的值为。

查看试题解析
18. 把四张大小相同的长方形卡片（如图①）按图②、图③两种放法放在一个底面为长方形（长比宽多6）的盒底上，底面未被卡片覆盖的部分用阴影表示，若记图②中阴影部分的周长为C₂ ，图③中阴影部分的周长为C₃ ，则C₂-C₃=.

查看试题解析

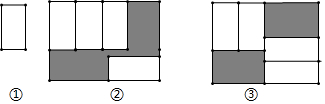
三、解答题

19. 化简与求值：

(1)、化简： $3 a - 2 - 4 a + 5$

(2)、化简： $(5 x^{2} - 3 y) - 3 (x^{2} - 2 y)$

(3)、先化简，再求值： $2 (2 a^{2} + 3 a b) - 3 (a^{2} + a b - \frac{2}{3})$ ，其中 $a = - 6$ ， $b = \frac{2}{3}$ ．

查看试题解析
20. 如图是火箭模型截面图，上面是三角形，中间是长方形，下面是梯形.

(1)、用含有a、b的代数式表示该截面的面积S；（需化简）

(2)、当a＝8cm，b＝5cm时，求这个截面图的面积.

查看试题解析
21. 已知 $A = 3 x^{2} + 3 y^{2} - 5 xy$ ， $B = 2 xy - 3 y^{2} + 4 x^{2}$ ．

(1)、化简： $2 B - A$ ；

(2)、已知 $- a^{| x - 2 |} b^{2}$ 与 $\frac{1}{3} {ab}^{y}$ 的同类项，求 $2 B - A$ 的值．

查看试题解析
22. 已知x＝2，y＝﹣1，求2[ $\frac{3}{2}$ x²y $- \frac{1}{2}$ （x+1）]﹣3（x²y﹣2y）﹣6（y $+ \frac{2}{3}$ ）的值时，马虎同学将x＝2，y＝﹣1错抄成y＝2，y＝1，可结果还是正确的，马虎同学比较纳闷，请你帮助他揭开其中的迷雾，写出你的说明过程．

查看试题解析
23. 有理数a，b，c在数轴上对应的点分别为A，B，C，如图，请你化简 $| c | - 2 | c + b | + 3 | a - c | - 4 | b + a |$ .

查看试题解析
24. 老师设计了一个数学实验，给甲、乙、丙三名同学各一张写有已化为最简的代数式的卡片，规则是两位同学的代数式相减等于第三位同学的代数式，则实验成功．甲、乙、丙的卡片如下，丙的卡片有一部分看不清楚了。

(1)、计算出甲减乙的结果，并判断甲减乙能否使实验成功；

(2)、嘉琪发现丙减甲可以使实验成功，请求出丙的代数式．

查看试题解析
25. 某农民2016年承包荒山若干亩，今年种西瓜总产量为56000千克．
假设西瓜在市场上每千克a元，在西瓜地里直接卖每千克b元．如果在西瓜地里直接卖没有费用产生；如果将西瓜拉到市场出售，平均每天售出2000千克，且需要10人帮忙，每人每天付工资100元，运费和各项税费平均每天300元．

(1)、分别用含a、b的代数式表示采用两种方式出售西瓜的收入；

(2)、若a=2，b=1.5，且两种出售方式都在相同时间内全部售完，请你通过计算说明选择那种出售方式较好？

查看试题解析

26. 南方A市想把30吨容易变质的水果运往B市销售，共有火车和汽车两种运输方式，现只可选择其中的一种，所涉及到的主要参考数据如下表所示： (注：“4元/吨·千米”表示每吨货物每千米需运费4元，以下“200 元/小时·吨”的意思类似)

运输工具	运输速度(千米/时)	运输费用(元/吨·千米)	装卸费用(元)	装卸时间(小时)
火车	100	4	2400	4
汽车	50	8	1200	2

这批水果在运输(包括装卸)过程中的损耗费为200元/小时·吨，若A、B两市间的距离为x千米。

(1)、用x的代数式分别表示火车运输方式和汽车运输方式的运输费用；

(2)、用x的代数式分别表示火车运输方式和汽车运输方式的损耗费；

(3)、若A、B两市间的距离为200千米时，两种运输方式总费用哪种较省？(总费用包括运输费用、装卸费用及损耗费用)

查看试题解析