2017年四川省广元市中考数学试卷

试卷更新日期：2017-10-10 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣ $\frac{1}{5}$ 的相反数是（）

A、﹣5 B、5 C、﹣ $\frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 根据央视报道，去年我国汽车尾气排放总量大约为47 000 000吨．将47 000 000用科学记数法表示为（）

A、0.47×10⁸ B、4.7×10⁷ C、47×10⁷ D、4.7×10⁶

查看试题解析
3. 下列运算正确的是（）

A、a²•a³=a⁶ B、2a²+a²=3a⁴ C、a⁶÷a³=a² D、（ab²）³=a³b⁶

查看试题解析
4. 数据21、12、18、16、20、21的众数和中位数分别是（）

A、21和19 B、21和17 C、20和19 D、20和18

查看试题解析
5. 把一块直尺与一块三角板如图放置，若∠1=45°，则∠2的度数为（）

A、115° B、120° C、145° D、135°

查看试题解析
6. 将五个相同的小正方体堆成如图所示的物体，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
7. 方程2x²﹣5x+3=0的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、两根异号

查看试题解析
8. 一元一次不等式组 ${\begin{matrix} x - 2 \leq 0 \\ 1 + \frac{1}{3} x > 0 \end{matrix}$ 的解集在数轴上表示出来，正确的是（）

A、 B、 C、 D、

查看试题解析
9. 为了节能减排，鼓励居民节约用电，某市出台了新的居民用电收费标准：（1）若每户居民每月用电量不超过100度，则按0.60元/度计算；（2）若每户居民每月用电量超过100度，则超过部分按0.8元/度计算（未超过部分仍按每度电0.60元/度计算），现假设某户居民某月用电量是x（单位：度），电费为y（单位：元），则y与x的函数关系用图象表示正确的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为F，连结DF，下列四个结论：①△AEF∽△CAB；②tan∠CAD= $\sqrt{2}$ ；③DF=DC；④CF=2AF，正确的是（）

A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析

二、填空题

11. 因式分解2x²﹣4x+2= ．

查看试题解析
12. 在平面直角坐标系中，将P（﹣3，2）向右平移2个单位，再向下平移2个单位得点P′，则P′的坐标为．

查看试题解析
13. 在函数y= $\sqrt{\frac{1}{x - 1}}$ 中，自变量x的取值范围是．

查看试题解析
14. 已知⊙O的半径为10，弦AB∥CD，AB=12，CD=16，则AB和CD的距离为．

查看试题解析
15. 已知二次函数y=ax²+bx+c的图象如图所示，有下列结论：①abc＜0；②a+c＞b；③3a+c＜0；④a+b＞m（am+b）（其中m≠1），其中正确的结论有．

查看试题解析

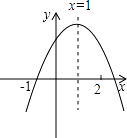
三、解答题

16. 计算|﹣2 $\sqrt{2}$ |﹣（ $\frac{1}{2}$ ）^﹣¹+（2017﹣π）⁰﹣ $\sqrt{8}$ •tan45°．

查看试题解析
17. 先化简，再求值： $\frac{1 - a}{a^{2} + a}$ ÷（ $\frac{1 - a}{a}$ ﹣a+1），其中，a= $\sqrt{2}$ ﹣1．

查看试题解析
18. 如图，在▱ABCD中，点E是AB边的中点，DE的延长线与CB的延长线交于点F．
求证：BC=BF．

查看试题解析
19. 为了解某校落实新课改精神的情况，现以该校九年级二班的同学参加课外活动的情况为样本，对其参加“球类”、“绘画类”、“舞蹈类”、“音乐类”、“棋类”活动的情况进行调查统计，并绘制了如图所示的统计图．

(1)、参加音乐类活动的学生人数为人，参加球类活动的人数的百分比为；

(2)、请把图2（条形统计图）补充完整；

(3)、该校学生共600人，则参加棋类活动的人数约为；

(4)、该班参加舞蹈类活动的4位同学中，有1位男生（用E表示）和3位女生（分别用F，G，H表示），先准备从中选取两名同学组成舞伴，请用列表或画树状图的方法求恰好选中一男一女的概率．

查看试题解析
20. 如图，某煤矿因不按规定操作发生瓦斯爆炸，救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A，B两个探测点探测到地下C处有生命迹象．已知A，B两点相距8米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C的深度（结果保留根号）．

查看试题解析
21. 某市教育局对某镇实施“教育精准扶贫”，为某镇建中、小型两种图书室共30个．计划养殖类图书不超过2000本，种植类图书不超过1600本．已知组建一个中型图书室需养殖类图书80本，种植类图书50本；组建一个小型图书室需养殖类图书30本，种植类图书60本．

(1)、符合题意的组建方案有几种？请写出具体的组建方案；

(2)、若组建一个中型图书室的费用是2000元，组建一个小型图书室的费用是1500元，哪种方案费用最低，最低费用是多少元？

查看试题解析
22. 如图，一次函数y=ax+b的图象与反比例函数y= $\frac{k}{x}$ 的图象交于C，D两点，与x，y轴交于B，A两点，且tan∠ABO= $\frac{1}{2}$ ，OB=4，OE=2．

(1)、求一次函数的解析式和反比例函数的解析式；

(2)、求△OCD的面积；

(3)、根据图象直接写出一次函数的值大于反比例函数的值时，自变量x的取值范围．

查看试题解析
23. 如图，在⊙O中，直径AB经过弦CD的中点E，点M在OD上，AM的延长线交⊙O于点G，交过D的直线于F，∠1=∠2，连结BD与CG交于点N．

(1)、求证：DF是⊙O的切线；

(2)、若点M是OD的中点，⊙O的半径为3，tan∠BOD=2 $\sqrt{2}$ ，求BN的长．

查看试题解析
24. 如图，已知抛物线y=ax²+bx+c过点A（﹣3，0），B（﹣2，3），C（0，3），其顶点为D．

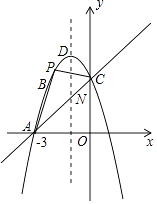(1)、求抛物线的解析式；

(2)、设点M（1，m），当MB+MD的值最小时，求m的值；

(3)、若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值；

(4)、若抛物线的对称轴与直线AC相交于点N，E为直线AC上任意一点，过点E作EF∥ND交抛物线于点F，以N，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．

查看试题解析