初中数学苏科版七年级上学期期末复习专题4 有理数的混合运算（含乘方）

试卷更新日期：2020-12-10 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列各组数中，互为相反数是（）

A、3²与－2³ B、－2³与（－2）³ C、－3²与（－3）² D、（－3×2）³与2³×（－3）

查看试题解析
2. 下列说法正确的是（）

A、对任何有理数a总有|a|＝a B、两个有理数的和一定大于每一个加数 C、任何数的平方总是正数 D、正数的任何正整数幂一定是正数

查看试题解析
3. 从2019年末到2020年5月2日截止，世界各国感染新冠状肺炎病毒患者达到3315003人，将数据3315003四舍五入精确到万位，用科学记数法表示为（）

A、332×10⁴ B、3.31×10⁶ C、3.32×10⁶ D、3.315×10⁶

查看试题解析
4. 计算（﹣0.25）²⁰²⁰×（﹣4）²⁰¹⁹的结果是（　　）

A、﹣4 B、4 C、﹣ $\frac{1}{4}$ D、 $\frac{1}{4}$

查看试题解析
5. 已知a、b互为相反数，e的绝对值为2，m与n互为倒数，则 $\frac{a + b}{3}$ +e²-4mn的值为（）

A、1 B、 $\frac{1}{3}$ C、0 D、无法确定

查看试题解析
6. 计算机是将信息转换成二进制数进行处理的.二进制即“逢二进一”，如 ${(1101)}_{2}$ 表示二进制数，将它转换成十进制形式是 $1 \times 2^{3} + 1 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^{0} = 13$ ，那么将二进制 ${(1111)}_{2}$ 转换成十进制形式是数（）

A、8 B、15 C、20 D、30

查看试题解析

7. 一家健身俱乐部收费标准为180元/次，若购买会员年卡，可享受如下优惠：

会员年卡类型	办卡费用（元）	每次收费（元
A类	1500	100
B类	3000	60
C类	4000	40

例如，购买A类会员年卡，一年内健身20次，消费1500+100×20=3500元.若一年内在该健身俱乐部健身的次数介于50-60次之间，则最省钱的方式为（）

A、购买C类会员年卡 B、购买B类会员年卡 C、购买A类会员年卡 D、不购买会员年卡

查看试题解析

8. 计算 $(1 - \frac{1}{2}) \times (1 - \frac{1}{3}) \times (1 - \frac{1}{4}) \times (1 - \frac{1}{5}) \cdot \cdot \cdot (1 - \frac{1}{20})$ 等于（）

A、 $\frac{1}{19}$ B、 $\frac{1}{20}$ C、 $\frac{19}{20}$ D、 $\frac{21}{20}$

查看试题解析
9. 计算 $\frac{1}{1^{2} + 1} + \frac{1}{2^{2} + 2} + \frac{1}{3^{2} + 3} + ··· + \frac{1}{2015^{2} + 2015}$ 的结果为（）

A、 $1$ B、 $\frac{2014}{2015}$ C、 $\frac{2015}{2016}$ D、 $\frac{2016}{2015}$

查看试题解析
10. 为求1＋2＋2²＋2³＋…＋2²⁰⁰⁸的值，可令S＝1＋2＋2²＋2³＋…＋2²⁰⁰⁸ ，则2S＝2＋2²＋2³＋2⁴＋…＋2²⁰⁰⁹ ，因此2S－S＝2²⁰⁰⁹－1，所以1＋2＋2²＋2³＋…＋2²⁰⁰⁸＝2²⁰⁰⁹－1．仿照以上推理计算出1＋3＋3²＋3³＋…＋3²⁰¹⁸的值是（）

A、3²⁰¹⁹－1 B、3²⁰¹⁸－1 C、 $\frac{3^{2019} - 1}{2}$ D、 $\frac{3^{2018} - 1}{2}$

查看试题解析

二、填空题

11. ${(- 1)}^{2 n} + {(- 1)}^{2 n + 1}$ =(n为正整数).

查看试题解析
12. 计算： $(- 12) \div (\frac{1}{2} + \frac{1}{3} - \frac{1}{4} - \frac{1}{6}) =$ .

查看试题解析
13. 如图是一个数值转换机，若输入a的值为 $- 3$ ，则输出的结果应为.

查看试题解析
14. 一天，小红与小丽利用温差测量山的高度，小红在山顶测得温度是 $- 4^{°} C$ ，小丽此时在山脚测得温度是 $4^{°} C$ .已知该地区高度每增加100米，气温大约降低 ${0.8}^{°} C$ ，这座山的高度大约是米.

查看试题解析
15. 如果规定符号“﹡”的意义是a﹡b= $\frac{a b}{a + b}$ ，那么 $(- 3)$ ﹡4的值为。

查看试题解析
16. 如图，方格表中的格子填上了数，每一行每一列及两条对角线中所填数的和均相等，则x的值是.

查看试题解析
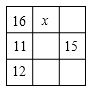17. 一张长方形的纸对折，如图所示可得到一条折痕（图中虚线），继续对折，对折时每次折痕与上次的折痕保持平行，连续对折2次后，可以得3条折痕，那么对折4次可以得到条折痕.

查看试题解析
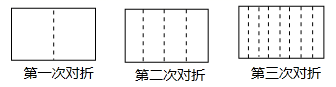18. 某校利用二维码进行学生学号统一编排．黑色小正方形表示1，白色小正方形表示0，将每一行数字从左到右依次记为a，b，c，d，那么利用公式a×2³+b×2²+c×2¹+d计算出每一行的数据．第一行表示年级，第二行表示班级，第三行表示班级学号的十位数，第四行表示班级学号的个位数．如图1所示，第一行数字从左往右依次是1，0，0，1，则表示的数据为1×2³+0×2²+0×2¹+1=9，计作09，第二行数字从左往右依次是1，0，1，0，则表示的数据为1×2³+0×2²+1×2¹=10，计作10，以此类推，图1代表的统一学号为091034，表示9年级10班34号．小明所对应的二维码如图2所示，则他的统一学号为．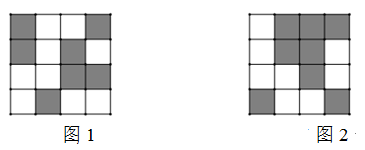

查看试题解析

三、解答题

19. 计算

(1)、 $5 \frac{3}{5} + (- 5 \frac{2}{3}) + 4 \frac{2}{5} + (- \frac{1}{3})$

(2)、 $(1 \frac{3}{4} - \frac{7}{8} - \frac{7}{16}) \times (- \frac{8}{7})$

(3)、 $| - \frac{3}{2} | \times [- 3^{2} \div {(- \frac{3}{2})}^{2} + {(- 2)}^{3}]$

(4)、 $- 1^{4} - (1 - 0.5) \times \frac{1}{3} \times [2 - {(- 3)}^{2}]$

查看试题解析
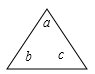20. 若“三角” 表示适算a+b+c，“方框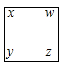表示运算x-y+z+w.
求：表示的速算，并计算结果。

查看试题解析
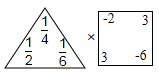21. 某服装店以每件82元的价格购进了30套保暖内衣，销售时，针对不同的顾客，这30套保暖内衣的售价不完全相同，若以100元为标准，将超过的钱数记为正，不足的钱数记为负，则记录结来如表所示：

售出件数

7

6

7

8

2

售价（元）

+5

+1

0

﹣2

﹣5

请你求出该服装店在售完这30套保暖内衣后，共赚了多少钱？

查看试题解析
22. 德国天文学家贝塞尔推出天鹅座第61颗暗星距地球102 000 000 000 000千米，是太阳到地球距离的690 000倍.用科学记数法表示这两个数.光在真空中每秒可行300 000千米，从天鹅座第61颗暗星发射的光线到达地球需多长时间（结果保留整数，1年按365天计算）？

查看试题解析
23. 如图，已知A、B两地在数轴上相距20米，A地在数轴上表示的点为-8，小乌龟从A地出发沿数轴往B地方向前进，第一次前进1米，第二次后退2米，第三次再前进3米，第四次又后退4米，……，按此规律行进，（数轴的一个单位长度等于1米）

(1)、求B地在数轴上表示的数；

(2)、若B地在原点的左侧，经过第五次行进后小乌龟到达点P，第六次行进后到达点Q，则点P和点Q到点A的距离相等吗？请说明理由；

(3)、若B地在原点的右侧，那么经过30次行进后，小乌龟到达的点与点B之间的距离是多少米？

查看试题解析
24. 如图，在数轴上点 $A$ 表示的数是 $- 3 ；$ 点 $B$ 在点 $A$ 的右侧，且到点 $A$ 的距离是18；点 $C$ 在点 $A$ 与点 $B$ 之间，且到点 $B$ 的距离是到点 $A$ 距离的2倍.

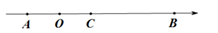
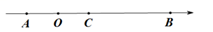(1)、点 $B$ 表示的数是；点 $C$ 表示的数是；

(2)、若点P从点 $A$ 出发，沿数轴以每秒4个单位长度的速度向右匀速运动；同时，点Q从点B出发，沿数轴以每秒2个单位长度的速度向左匀速运动。设运动时间为 $t$ 秒，在运动过程中，当 $t$ 为何值时，点P与点Q之间的距离为6？

(3)、在（2）的条件下，若点P与点C之间的距离表示为PC，点Q与点B之间的距离表示为 $Q B ，$ 在运动过程中，是否存在某一时刻使得 $P C + Q B = 4$ ？若存在，请求出此时点 $P$ 表示的数；若不存在，请说明理由.

查看试题解析
25. 定义：若A，B，C为数轴上三点，若点C到点A的距离是点C到点B的距离2倍，我们就称点C是【A，B】的美好点．
例如：如图1，点A表示的数为-1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是【A，B】的美好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是【A，B】的美好点，但点D是【B，A】的美好点．

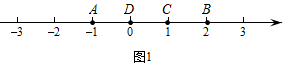
如图2，M，N为数轴上两点，点M所表示的数为-7，点N所表示的数为2．

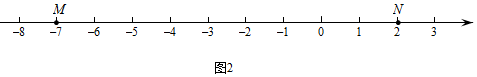(1)、点E，F，G表示的数分别是-3，6.5，11，其中是【M，N】美好点的是；写出【N，M】美好点H所表示的数是．

(2)、现有一只电子蚂蚁P从点N开始出发，以2个单位每秒的速度向左运动．当t为何值时，P，M和N中恰有一个点为其余两点的美好点？

查看试题解析
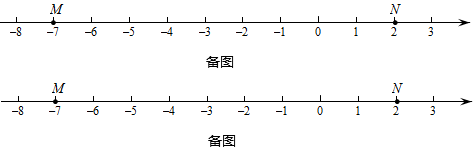26. 图1是由若干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了 $n$ 层，将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为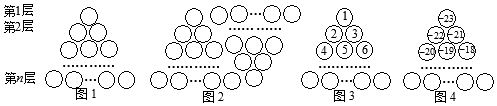 $1 + 2 + 3 + \dots + n = \frac{n (n + 1)}{2} .$

如果图中的圆圈共有13层，请解决下列问题：

(1)、若自上往下，在图①每个圆圈中填上一串连续的正整数1，2，3，4，…，得到图3，写出第11层最左边这个圆圈中的数；

(2)、若自上往下，在图①每个圆圈中填上一串连续的整数-23，-22，-21，20，…，得到图4，写出第10层最右边圆圈内的数；

(3)、根据以上规律，求图4中第1层到第10层所有圆圈中各数之和(写出计算过程).

查看试题解析

售出件数	7	6	7	8	2
售价（元）	+5	+1	0	﹣2	﹣5