2017年四川省阿坝州中考数学试卷
试卷更新日期:2017-10-10 类型:中考真卷
一、选择题
-
1. ﹣2的倒数是( )
A、﹣2 B、﹣ C、 D、22. 如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是( ) A、
A、 B、
B、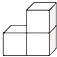 C、
C、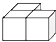 D、
D、 3. 下列计算正确的是( )A、a3+a2=2a5 B、a3•a2=a6 C、a3÷a2=a D、(a3)2=a94. 已知一个正多边形的一个外角为36°,则这个正多边形的边数是( )A、8 B、9 C、10 D、115. 对“某市明天下雨的概率是75%”这句话,理解正确的是( )
3. 下列计算正确的是( )A、a3+a2=2a5 B、a3•a2=a6 C、a3÷a2=a D、(a3)2=a94. 已知一个正多边形的一个外角为36°,则这个正多边形的边数是( )A、8 B、9 C、10 D、115. 对“某市明天下雨的概率是75%”这句话,理解正确的是( )
A、某市明天将有75%的时间下雨 B、某市明天将有75%的地区下雨 C、某市明天一定下雨 D、某市明天下雨的可能性较大6. 如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( ) A、20° B、35° C、45° D、70°7. 如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
A、20° B、35° C、45° D、70°7. 如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )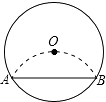 A、2cm B、 cm C、2 cm D、2 cm8. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
A、2cm B、 cm C、2 cm D、2 cm8. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )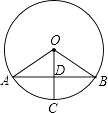 A、2 B、3 C、4 D、59. 如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A、2 B、3 C、4 D、59. 如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( ) A、msin35° B、mcos35° C、 D、10. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
A、msin35° B、mcos35° C、 D、10. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 因式分解:2x2﹣18= .12. 数据1,2,3,0,﹣3,﹣2,﹣1的中位数是 .13. 某种电子元件的面积大约为0.00000069平方毫米,将0.00000069这个数用科学记数法表示为 .14. 若一元二次方程x2+4x+c=0有两个相等的实数根,则c的值是 .15. 在函数y= 中,自变量x的取值范围是 .
三、解答题
-
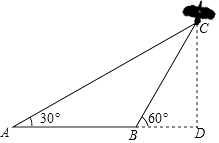
16. 计算题(1)、计算:( ﹣2)0+( )﹣1+4sin60°﹣|﹣ |.(2)、先化简,再求值:(1﹣ )÷ ﹣ ,其中x2+2x﹣1=0.17. 如图,小明在A处测得风筝(C处)的仰角为30°,同时在A正对着风筝方向距A处30米的B处,小明测得风筝的仰角为60°,求风筝此时的高度.(结果保留根号)
 18. 某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.
18. 某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.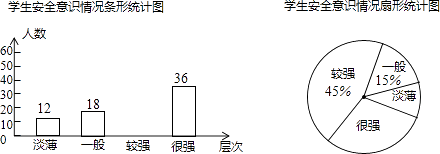
根据以上信息,解答下列问题:
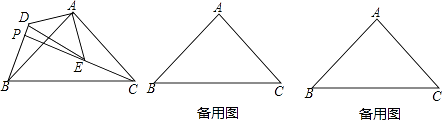
(1)、这次调查一共抽取了名学生,其中安全意识为“很强”的学生占被调查学生总数的百分比是;(2)、请将条形统计图补充完整;(3)、该校有1800名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有名.19. 如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB= ,直线l上的点P位于y轴左侧,且到y轴的距离为1.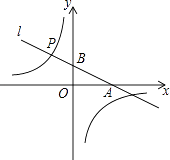 (1)、求直线l的表达式;(2)、若反比例函数y= 的图象经过点P,求m的值.20. 如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)、求直线l的表达式;(2)、若反比例函数y= 的图象经过点P,求m的值.20. 如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.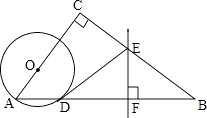 (1)、判断直线DE与⊙O的位置关系,并说明理由;(2)、若AC=6,BC=8,OA=2,求线段DE的长.
(1)、判断直线DE与⊙O的位置关系,并说明理由;(2)、若AC=6,BC=8,OA=2,求线段DE的长.四、填空题
-
21. 在一个不透明的空袋子里,放入仅颜色不同的2个红球和1个白球,从中随机摸出1个球后不放回,再从中随机摸出1个球,两次都摸到红球的概率是 .22. 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .
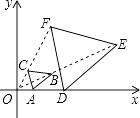 23. 如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y= 的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k= .
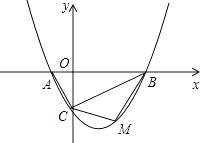
23. 如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y= 的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k= .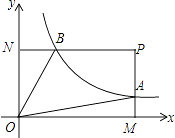 24. 如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 .
24. 如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 .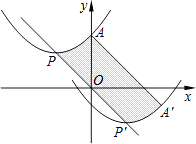 25. 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2017的坐标是 .
25. 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2017的坐标是 .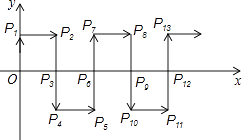
五、解答题:
-
26. 某商品的进价为每件40元,售价为每件60元时,每个月可卖出100件;如果每件商品的售价每上涨1元,则每个月少卖2件.设每件商品的售价为x元(x为正整数),每个月的销售利润为y元.
(1)、当每件商品的售价是多少元时,每个月的利润刚好是2250元?(2)、当每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?