初中数学苏科版七年级上学期期末复习专题2 绝对值与相反数

试卷更新日期：2020-12-10 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列各组数中，互为相反数的一组是（）

A、-3与+（-3） B、3与|-3| C、+3与-|+3| D、+（-3）与-|-3|

查看试题解析
2. 下列说法：①互为相反数的两个数绝对值相等；②绝对值等于本身的数只有正数，③不相等的两个数绝对值不相等；④绝对值相等的两数一定相等．其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
3. 在数轴上，点 $A ， B$ 在原点 $O$ 的同侧，分别表示数 $1, a$ ，将点 $A$ 向左平移 $3$ 个单位长度，得到点 $C$ ，点 $C$ 与点 $B$ 所表示的数互为相反数，则 $a$ 的值为（）

A、3 B、2 C、-1 D、0

查看试题解析
4. 已知|a|=5，|b|=2，且|a﹣b|=b﹣a，则a+b=（）

A、3或7 B、﹣3或﹣7 C、﹣3 D、﹣7

查看试题解析
5. 现有四种说法：①-a表示负数；②若|x|=-x，则x<0；③绝对值最小的有理数是0；④若|a|=|b|，则a=b；⑤若a<b<o，则|a|>|b|，其中正确的是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 已知： $a ， b$ 为有理数，且 $a < b < 0$ ，那么 $| a |$ 与 $| b |$ 的大小关系是（）

A、 $| a | > | b |$ B、 $| a | = | b |$ C、 $| a | < | b |$ D、 $| a | \geq | b |$

查看试题解析
7. 有理数a、b在数轴上的位置如图所示，则下列结论中正确的是（）

A、a+b＞0 B、ab＞0 C、a﹣b＜o D、a÷b＞0

查看试题解析
8. 有理数 $a ， b$ 在数轴上的对应点如图所示，则下面式子中正确的个数是（）
①b＜0＜a；②|b|＜|a|；③ab＞0；④a-b＞a+b．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如果 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ ＝﹣1，那么 $\frac{| a b |}{a b} + \frac{| b c |}{b c} + \frac{| a c |}{a c} + \frac{| a b c |}{a b c}$ 的值为（）

A、﹣2 B、﹣1 C、0 D、不确定

查看试题解析
10. 不相等的有理数a，b，c在数轴上的对应点分别是A，B，C，如果 $| a - b | + | b - c | = | a - c |$ ，那么点B $($ $)$

A、在A，C点的左边 B、在A，C点的右边 C、在A，C点之间 D、上述三种均可能

查看试题解析

二、填空题

11. 在 $3.5$ ， $- 3 \frac{1}{2}$ ，0， $- 8$ 这四个数中，最小的数是，最大的数是，绝对值最大的数是，互为相反数的两个数是和 .

查看试题解析
12. $| - a | = | - 3 |$ ，则 $a$ =.

查看试题解析
13. 两个数和的绝对值是17，一个数是－5，另一个数是。

查看试题解析
14. 若 $3 a + 4$ 与 $2 b - 6$ 互为相反数，则 $4 b + 6 a$ 的值为．

查看试题解析
15. 有理数a、b、c在数轴上的对应点如图，化简代数式：|a-b|+|a+b|-2|c-a|= ．

查看试题解析
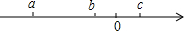16. 已知 $a$ , $b$ 为有理数，且 $a > 0$ , $b < 0$ , $a + b < 0$ ,将四个数 $a$ , $b$ , $- a$ , $- b$ 按由小到大的顺序排列是

查看试题解析
17. 如图A，B，C，D，E分别是数轴上五个连续整数所对应的点，其中有一点是原点，数a对应的点在B与C之间，数b对应的点在D与E之间，若 $| a | + | b | = 3$ 则原点可能是．

查看试题解析
18. 若 $| \begin{matrix} x - 3 \end{matrix} |$ ＋ $| \begin{matrix} x + 2 \end{matrix} |$ 的值最小，则x的取值范围是．

查看试题解析

三、综合题

19. 阅读：因为一个非负数的绝对值等于它本身，负数的绝对值等于它的相反数。所以，当a⩾0时，|a|=a，当a⩽0时，|a|=−a.根据以上阅读完成：

(1)、|3.14−π|=；

(2)、计算： $| \frac{1}{3} - \frac{1}{2} | + | \frac{1}{4} - \frac{1}{3} | + | \frac{1}{5} - \frac{1}{4} | + ... + | \frac{1}{2000} - \frac{1}{1999} |$

查看试题解析
20. 已知有理数a、b在数轴上的对应点如图所示.

(1)、已知a= –2，b=0.3，计算|a+b|–|a|–|1–b|的值；

(2)、已知有理数a、b，计算|a+b|–|a|–|1–b|的值.

查看试题解析
21.

(1)、比较下列各式的大小:
|5|+|3||5+3|，|-5|+|-3||（-5）+（-3）|，

|-5|+|3||（-5）+3|，|0|+|-5||0+（-5）|；

(2)、通过（1）的比较、观察，请你猜想归纳:
当a，b为有理数时，|a|+|b||a+b|（填入“≥”“≤”“>”或“<”）；

(3)、根据（2）中你得出的结论，求当|x|+|-2|=|x-2|时，直接写出x的取值范围.

查看试题解析
22. 已知：b是最小的正整数，且a、b满足|c-6|+|a+b|=0，请回答问题：

(1)、请直接写出a、b、c的值，a= ， b= ， c= 。

(2)、a、b、c所对应的点分别为A、B、C，点P为一动点，其对应的数为x点P在A、B之间运动时，请化简式子：|x+1|-|x-1|-2|x+5|(请写出化简过程)

(3)、在(1)(2)的条件下，点A、B、C开始在数轴上运动，若点A以每秒n（n>0)个单位长度的速度向左运动，同时，点B和点C分别以每秒2n个单位长度和5n个单位长度的速度向右运动，假设经过t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB．请问：
BC-AB的值是否随着时间的变化而改变?若变化，请说明理由：若不变，请求其值。

查看试题解析
23. 阅读下面材料：点A、B在数轴上分别表示有理数a、b ， A、B两点之间的距离表示为AB ，在数轴上A、B两点之间的距离AB＝|a﹣b|．回答下列问题：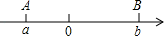

(1)、数轴上表示﹣3和1两点之间的距离是，数轴上表示﹣2和3的两点之间的距离是；

(2)、数轴上表示x和﹣1的两点之间的距离表示为；

(3)、若x表示一个有理数，则|x﹣2|+|x+3|有最小值吗？若有，请求出最小值；若没有，请说明理由．

查看试题解析
24. 已知数轴上有A，B，C三点，分别代表－24，－10，10，电子蚂蚁D从A出发沿数轴的正方向爬行，速度为4个单位/秒.

(1)、A，B两点的距离AB= ， A，C两点的距离AC= ， B，C两点的距离BC=；

(2)、电子蚂蚁D从A出发沿数轴的正方向爬行3秒后，点D对应的数是；

(3)、电子蚂蚁D从A出发沿数轴的正方向爬行多少秒后，到A，B，C的距离和为40个单位？

查看试题解析
25. 在学习绝对值后，我们知道， $| a |$ 表示数 $a$ 在数轴上的对应点与原点的距离. 如： $| 5 |$ 表示5在数轴上的对应点到原点的距离．而 $| 5 | = | 5 - 0 |$ ，即 $| 5 - 0 |$ 表示5、0在数轴上对应的两点之间的距离.类似的，有： $| 5 - 3 |$ 表示5、3在数轴上对应的两点之间的距离； $| 5 + 3 | = | 5 - (- 3) |$ ，所以 $| 5 + 3 |$ 表示5、 $- 3$ 在数轴上对应的两点之间的距离. 一般地，点A、B在数轴上分别表示有理数 $a$ 、 $b$ ，那么A、B之间的距离可表示为 $| a - b |$ ．
请根据绝对值的意义并结合数轴解答下列问题：

(1)、数轴上表示2和5的两点之间的距离是；数轴上表示1和－3的两点之间的距离是；

(2)、数轴上P、Q两点的距离为3，且点P表示的数是2，则点Q表示的数是.

(3)、点A、B、C在数轴上分别表示有理数 $x$ 、 $- 3$ 、1，那么A到B的距离与A到C的距离之和可表示为；

(4)、满足 $| x - 3 | + | x + 2 | = 5$ 的整数 $x$ 的值为.

(5)、 $| x - 1 | + | x - 2 | + | x - 3 | + \cdot \cdot \cdot + | x - 100 |$ 的最小值为.

查看试题解析
26. 已知数轴上，一动点Q从原点O出发，沿数轴以每秒2个单位长度的速度来回移动，其移动的方式是：先向右移动1个单位长度，再向左移动2个单位长度，又向右移动3个单位长度，再向左移动4个单位长度，又向右移动5个单位长度…，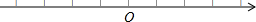

(1)、动点Q运动3秒时，求此时Q在数轴上表示的数?

(2)、当动点Q第一次运动到数轴上对应的数为10时，求Q运动的时间t；

(3)、若5秒时，动点Q激活所在位置P点，P点立即以0.1个单位长度/秒的速度沿数轴运动，试求点P激活后第一次与继续运动的点Q相遇时所在的位置.

查看试题解析