初中数学苏科版七年级上学期期末复习专题1 有理数的分类及数轴

试卷更新日期：2020-12-10 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列说法中：
①0是最小的整数；②有理数不是正数就是负数；③正整数、负整数、正分数、负分数统称为有理数；④非负数就是正数；⑤ $- \frac{π}{2}$ 不仅是有理数，而且是分数；⑥ $\frac{23}{7}$ 是无限不循环小数，所以不是有理数；⑦无限小数不都是有理数；⑧正数中没有最小的数，负数中没有最大的数．

其中错误的说法的个数为（）

A、7个 B、6个 C、5个 D、4个

查看试题解析
2. 有下列关于“0”的说法：①0是正数和负数的分界；②0只表示“什么也没有”；③0可以表示特定的意义；④0是正数；⑤0是自然数；⑥0是非负数；⑦某地海拔为0 m表示没有海拔．其中正确的有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
3. 在数轴上，与表示－2的点距离等于3的点所表示的数是（）

A、3 B、3或-3 C、1 D、1和－5

查看试题解析
4. 如图图中数轴画法错误的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 设a 是最小的正整数，b是最大的负整数，c是绝对值最小的有理数，则a－b＋c 的值为（）

A、－1 B、0 C、1 D、2

查看试题解析
6. 数轴上点A和点B表示的数分别为－4和2，若要使点A到点B的距离是2，则应将点A向右移动（）

A、4个单位长度 B、6个单位长度 C、4个单位长度或8个单位长度 D、6个单位长度或8个单位长度

查看试题解析
7. 如图，数轴上 A ， B 两点分别对应有理数 a ， b ，则下列结论正确的是（）

A、a-b＞0 B、ab＞0 C、a+b＞0 D、|a|-|b|＞0

查看试题解析
8. 下列说法中，正确的个数有（）
①-lal一定是负数；

②过一点有且只有一条直线与已知直线平行；

③若一个数小于它的绝对值，则这个数是负数；

④若a=|b|，则a与b互为相反数；

⑤若|a|+a=0，则a是非正数

A、2个 B、3个 C、4个 D、5个

查看试题解析
9. 如图，数轴表示的是5个城市的国际标准时间（单位：时），如果北京的时间是2020年1月9日上午9时，下列说法正确的是（）

A、伦敦的时间是2020年1月9日凌晨1时 B、纽约的时间是2020年1月9日晚上20时 C、多伦多的时间是2020年1月8日晚上19时 D、汉城的时间是2020年1月9日上午8时

查看试题解析
10. 设三个互不相等的有理数，既可以表示为 $1 ， a + b ， a$ 的形式，也可以表示为 $0 ， \frac{b}{a}, b$ 的形式，则 $a^{2018} + b^{2018}$ 的值等于（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

11. 大-1 $\frac{1}{3}$ 于且小于 $2$ 的所有整数是.

查看试题解析
12. 一只小蚂蚁停在数轴上表示﹣3的点上，后来它沿数轴爬行5个单位长度，则此时小蚂蚁所处的点表示的数为．

查看试题解析
13. 数轴上表示整数的点称为整点．某数轴的单位长度是1厘米，若在这个数轴上随意画出一条长为2020厘米的线段 $A B$ ，则线段 $A B$ 盖住的整点个数是．

查看试题解析
14. 有理数a，b，c在数轴上的位置如图所示，化简|b+a|﹣|b﹣c|+|a﹣c|的结果是.

查看试题解析
15. 如图所示，一只蚂蚁从点 $A$ 沿着数轴向右爬了2个单位到达点 $B$ ，点 $A$ 表示的数为 $- \frac{1}{2}$ ，设点 $B$ 表示的数为 $m$ ，则代数式 $| m - 1 | + (m + 5)$ 的值为．

查看试题解析
16. 如图所示，M，N，P，R分别是数轴上的四个整数所对应的点，其中有一个点是原点，并且，MN=NP=PR=1，数a对应的点在M和N之间，数b对应的点在P和R之间，若|a|+|b|=2，则原点是（填M，N，P，R中的一个或几个）

查看试题解析
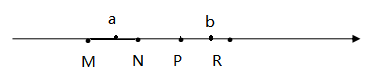17. 数轴上点 A，B 到表示−2 的点的距离都为 9，P 为线段 AB 上任一点，C，D 两点分别从 P，B 同时向 A 点移动，且 C 点运动速度为每秒 3 个单位长度，D 点运动速度为每秒 4 个单位长度，运动 3 秒时，CD=4，则 P 点表示的数为.

查看试题解析
18. 如图，数轴上，点A的初始位置表示的数为1，现点A做如下移动：第1次点A向左移动3个单位长度至点A₁ ，第2次从点A1向右移动6个单位长度至点A₂ ，第3次从点A₂向左移动9个单位长度至点A₃ ， …，按照这种移动方式进行下去，点A₄表示的数，是，如果点A_n与原点的距离不小于20，那么n的最小值是．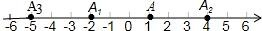

查看试题解析

三、综合题

19. 已知下列各数：8，-7.25， $\frac{9}{10}$ ， $\frac{π}{3}$ ，-301，0.010010001，0，2，10.9， $- 0. \overset{\cdot}{3}$ ， $-$ 25%．把它们填入相应的大括号内．
负数集合： ${\dots}$ ；

非负整数集合： ${\dots}$ ；

负分数集合： ${\dots}$ ；

正有理数集合： ${\dots}$ ．

查看试题解析
20. 出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的，如果规定向东为正，向西为负，他这天下午行车里程（单位：千米）如下：
+15，﹣2，+5，﹣1，+10，﹣3，﹣2，+12，+4，﹣5，+6

(1)、小李下午出发地记为0，他将最后一名乘客送抵目的地时，小李距下午出车时的出发地有多远？

(2)、若汽车耗油量为0.41升/千米，这天下午小李共耗油多少升？

查看试题解析
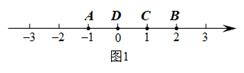
21. 小明骑车从家出发，先向东骑行2km到达A村，继续向东骑行3km到达B村.然后向西骑行9km 到达C村，最后回到家.

(1)、以家为原点.以向东方向为正方向.用1cm表示1km.画出数轴.并在数轴上表示出A、B、C三个村庄的位置.

(2)、C村离A村有多远？

(3)、小明一共行了多少km？

查看试题解析
22. 已知数轴上有A，B，C三点，分别代表－24，－10，10，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，甲的速度为4个单位／秒．

(1)、问多少秒后，甲到A，B，C的距离和为40个单位？

(2)、若乙的速度为6个单位／秒，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，问甲，乙在数轴上的哪个点相遇？

(3)、在（1）（2）的条件下，当甲到A、B、C的距离和为40个单位时，甲调头返回．问甲，乙还能在数轴上相遇吗？若能，求出相遇点；若不能，请说明理由．

查看试题解析
23. 定义：若A，B，C为数轴上三点，若点C到点A的距离是点C到点B的距离2倍，我们就称点C是（A，B）的美好点.
例如：如图1，点A表示的数为 $- 1$ ，点B表示的数为2.表示1的点C到点A的距离是2，到点B的距离是1，那么点C是（A，B）的美好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是（A，B）的美好点，但点D是（B，A）的美好点.

如图2，M，N为数轴上两点，点M所表示的数为 $- 7$ ，点N所表示的数为2.

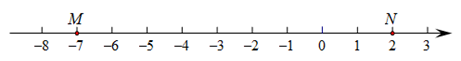
图2

备图

(1)、点E，F，G表示的数分别是 $- 3$ ，6.5，11，其中是（M，N）美好点的是；写出（N，M）美好点H所表示的数是.

(2)、现有一只电子蚂蚁P从点N开始出发，以2个单位每秒的速度向左运动. 当t为何值时，P，M和N中恰有一个点为其余两点的美好点？

查看试题解析
24. 结合数轴与绝对值的知识回答下列问题：

(1)、数轴上表示4和1的两点之间的距离是；表示－3和2两点之间的距离是；一般地，数轴上表示数m和数n的两点之间的距离等于 $| m - n |$ ．如果表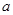示数和－2的两点之间的距离是3，那么 $a$ =；

(2)、若数轴上表示数 $a$ 的点位于－4与2之间，求 $| a + 4 |$ + $| a - 2 |$ 的值；

查看试题解析
25. 阅读材料，并回答问题
如图，有一根木棒 MN 放置在数轴上，它的两端 M、N 分别落在点 A、B．将木棒在数轴上水平移动，当点 M 移动到点 B 时，点 N 所对应的数为 20，当点 N 移动到点 A 时，点 M 所对应的数为 5．（单位：cm）

(1)、由此可得，木棒长为cm．

(2)、借助上述方法解决问题：一天，美羊羊去问村长爷爷的年龄，村长爷爷说：“我若是你现在这么大，你还要40年才出生呢，你若是我现在这么大，我已经是老寿星了，116岁了，哈哈！”美羊羊纳闷，村长爷爷到底是多少岁？请你画出示意图，求出村长爷爷和美羊羊现在的年龄，并说明解题思路．

查看试题解析
26. 已知，如图，A、B分别为数轴上的两点，A点对应的数为-20，B点对应的数为100.

(1)、请写出AB中点M对应的数。

(2)、现有一只电子蚂蚁P从B点出发，以6单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以4单位/秒的速度向右运动。设两只电子蚂蚁在数轴上的C点相遇，你知道C点对应的数是多少吗？

(3)、若当电子蚂蚁P从B点出发时，以6单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以4单位/秒的速度也向左运动。设两只电子蚂蚁在数轴上的D点相遇，你知道D点对应的数是多少吗？

查看试题解析