初中数学苏科版2020-2021学年九年级上学期期末模拟试卷
试卷更新日期:2020-12-10 类型:期末考试
一、单选题
-
1. 下列方程中,关于x的一元二次方程是( )A、ax2+bx+c=0 B、x2-x(x+7)=0 C、2x2-y-1=0 D、x2-2x-3=02. 下列说法中,不正确的个数是( )
①优弧一定比劣弧长;②面积相等的两个圆是等圆;③长度相等的弧是等弧;④经过圆心的一个定点可以作无数条弦;⑤经过圆内一定点可以作无数条直径.
A、1个 B、2个 C、3个 D、4个3. 某书店与一山区小学建立帮扶关系,连续6个月向该小学赠送书籍的数量分别如下(单位:本):300,200,200,300,300,500这组数据的众数、中位数、平均数分别是( )A、300,150,300 B、300,200,200 C、600,300,200 D、300,300,3004. 如图,随机闭合开关 , , 中的两个,则能让两盏灯泡同时发光的概率为( )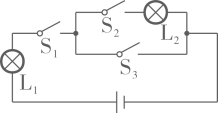 A、 B、 C、 D、5. 要使关于x的一元二次方程 有两个实数根,且使关于x的分式方程 的解为非负数的所有整数 的个数为( )A、5个 B、6个 C、7个 D、8个6. 设 、 是方程x2+x﹣2015=0的两个实数根,则 2+2 + 的值为( )A、2011 B、2012 C、2013 D、20147. 初三(3)班同学在临近毕业时,每一个同学都将自己的照片向全班其他同学各送一张以表示纪念,全班共送了1640张照片,如果设全班有x名学生,则根据题意,可列方程( )A、x(x+1)=1640 B、x(x-1)=1640 C、2x(x+1)=1640 D、x(x-1)=2×16408. 如图,把一个量角器与一块30°(∠CAB=30° )角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有点P恰好是量角器的半圆弧中点,连结CP。若BC=2,则CP的长为( )
A、 B、 C、 D、5. 要使关于x的一元二次方程 有两个实数根,且使关于x的分式方程 的解为非负数的所有整数 的个数为( )A、5个 B、6个 C、7个 D、8个6. 设 、 是方程x2+x﹣2015=0的两个实数根,则 2+2 + 的值为( )A、2011 B、2012 C、2013 D、20147. 初三(3)班同学在临近毕业时,每一个同学都将自己的照片向全班其他同学各送一张以表示纪念,全班共送了1640张照片,如果设全班有x名学生,则根据题意,可列方程( )A、x(x+1)=1640 B、x(x-1)=1640 C、2x(x+1)=1640 D、x(x-1)=2×16408. 如图,把一个量角器与一块30°(∠CAB=30° )角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有点P恰好是量角器的半圆弧中点,连结CP。若BC=2,则CP的长为( )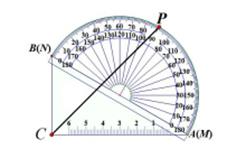 A、 B、 C、 D、9. 如图,在⊙O中,点C在优弧AB上,将弧BC沿BC折叠后刚好经过AB的中点D. 若⊙O的半径为 ,AB=8,则BC的长是( )
A、 B、 C、 D、9. 如图,在⊙O中,点C在优弧AB上,将弧BC沿BC折叠后刚好经过AB的中点D. 若⊙O的半径为 ,AB=8,则BC的长是( )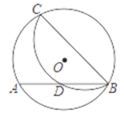 A、 B、 C、 D、10. 如图,等边 的边长为 ,以O为圆心, 为直径的半圆经过点A,连接 , 相交于点P,将等边 从 与 重合的位置开始,绕着点O顺时针旋转 ,交点P运动的路径长是( )
A、 B、 C、 D、10. 如图,等边 的边长为 ,以O为圆心, 为直径的半圆经过点A,连接 , 相交于点P,将等边 从 与 重合的位置开始,绕着点O顺时针旋转 ,交点P运动的路径长是( )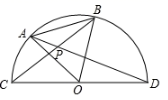 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知 是一元二次方程 的一个根,那么 的值是 .12. 一条弦所对的圆心角的度数为95°,这条弦所对的圆周角的度数为.13. 已知x1 , x2 , x3的平均数 =10,则2x1 , 2x2 , 2x3的平均数为.14. 小鸡孵化场孵化出一批小鸡,工人在其中50只小鸡上做记号后让这批小鸡充分跑散,后来再任意抓出100只小鸡,其中有记号的有10只,则这批小鸡大约有只。15. 如图,在 中, , , .若以 所在直线为轴,把 旋转一周,得到一个圆锥,则这个圆锥的侧面积等于.
 16. 如下图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ , 那么图中矩形AMKP的面积 与矩形QCNK的面积 的大小关系是 (填“>”或“<”或“=”).
16. 如下图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ , 那么图中矩形AMKP的面积 与矩形QCNK的面积 的大小关系是 (填“>”或“<”或“=”).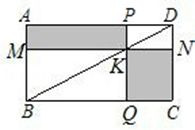 17. 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,现在从第一个位置翻滚到第三个位置,则B点所经过的路径长度为.
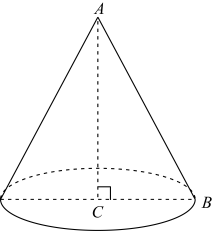
17. 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,现在从第一个位置翻滚到第三个位置,则B点所经过的路径长度为.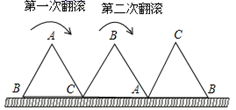 18. 如图,等边△AOB,点C是边AO所在直线上的动点,点D是x轴上的动点,在矩形CDEF中,CD=6,DE= ,则OF的最小值为.
18. 如图,等边△AOB,点C是边AO所在直线上的动点,点D是x轴上的动点,在矩形CDEF中,CD=6,DE= ,则OF的最小值为.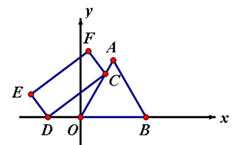
三、综合题
-
19. 按要求解方程(1)、 ,(因式分解法)(2)、 .(配方法)20. 选用适当的方法解下列方程:(1)、x2﹣6x=7(2)、21. 一只不透明袋子中装有 个白球和若干个红球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中任意摸出 个球,记下颜色后放回、搅匀,不断重复这个过程,获得数据如下:
摸球的次数 200 300 400 1000 1600 2000 摸到白球的频数 72 93 130 334 532 667 摸到白球的频率 0.3600 0.2100 0.3250 0.3340 0.3325 0.3335 (1)、该学习小组发现,摸到白球的频率在一个常数附近摆动,这个常数是(精确到0.01),由此估出红球有个.(2)、现从该袋中摸出2个球,请用树状图或列表的方法列出所有等可能的结果,并求恰好摸到1个白球,1个红球的概率.22. 已知关于x的一元二次方程(1)、求证:这个方程有两个不相等的实数根。(2)、如果这个方程的两个实数根分别是 ,且 ,求m的值。23. 如图, 是半圆O的直径, 是半圆O上不同于 的两点 与 相交于点 是半圆O所任圆的切线,与 的延长线相交于点E,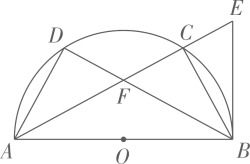 (1)、求证: ;(2)、若 求 平分 .24. 如图,在△ABC中,BC=4,且△ABC的面积为4,以点A为圆心,2为半径的⊙A交AB于E,交AC于F,点P是⊙A上一点,且∠EPF=45°.
(1)、求证: ;(2)、若 求 平分 .24. 如图,在△ABC中,BC=4,且△ABC的面积为4,以点A为圆心,2为半径的⊙A交AB于E,交AC于F,点P是⊙A上一点,且∠EPF=45°.
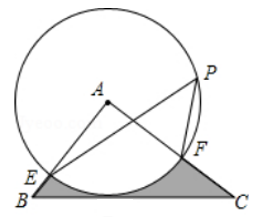 (1)、求证:BC为⊙A的切线;(2)、求图中阴影部分的面积.25. 阅读材料:各类方程的解法
(1)、求证:BC为⊙A的切线;(2)、求图中阴影部分的面积.25. 阅读材料:各类方程的解法求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想——转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)、问题:方程x3+x2-2x=0的解是x1=0,x2= , x3=;(2)、拓展:用“转化”思想求方程 =x的解;(3)、应用:如图,已知矩形草坪ABCD的长AD=8 m,宽AB=3 m,小华把一根长为10 m的绳子的一端固定在点B,沿草坪边BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边PD,DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.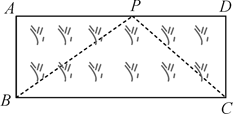 26. 定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
26. 定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.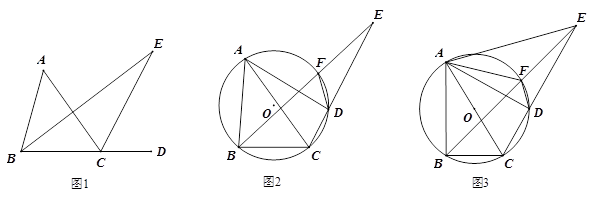 (1)、如图1,∠E是△ABC中A的遥望角,若 ,请用含a的代数式表示∠E.(2)、如图2,四边形ABCD内接于⊙O, ,四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)、如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.
(1)、如图1,∠E是△ABC中A的遥望角,若 ,请用含a的代数式表示∠E.(2)、如图2,四边形ABCD内接于⊙O, ,四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)、如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.①求∠AED的度数;
②若AB=8,CD=5,求△DEF的面积.