河北省邯郸市临漳县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2020-12-09 类型:期中考试
一、单选题
-
1. 的平方根是( )A、±3 B、3 C、9 D、±92. 如图,正方形ABCD的面积是( )
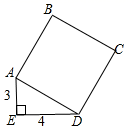 A、5 B、25 C、7 D、13. 如图,在边长为1个单位长度的小正方形组成的网格中,最长的线段是( )
A、5 B、25 C、7 D、13. 如图,在边长为1个单位长度的小正方形组成的网格中,最长的线段是( ) A、AB B、BC C、CD D、AE4. 下列各组数是勾股数的一组是( )A、7,24,25 B、 C、1.5,2,2.5 D、5. 在实数 , , ,0,-1.414, , ,0.101001000100001中,无理数有( )A、2个 B、3个 C、4个 D、5个6. 在平面直角坐标系中,点 关于原点对称点在()A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 下列选项中的整数,与 最接近的是( )A、3 B、4 C、5 D、68. 下列说法:
A、AB B、BC C、CD D、AE4. 下列各组数是勾股数的一组是( )A、7,24,25 B、 C、1.5,2,2.5 D、5. 在实数 , , ,0,-1.414, , ,0.101001000100001中,无理数有( )A、2个 B、3个 C、4个 D、5个6. 在平面直角坐标系中,点 关于原点对称点在()A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 下列选项中的整数,与 最接近的是( )A、3 B、4 C、5 D、68. 下列说法:①实数和数轴上的点是一一对应的;②无理数是开方开不尽的数;③负数没有立方根;④16的平方根是±4,用式子表示是 =±4;⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0,其中错误的是( )
A、0个 B、1个 C、2个 D、3个9. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、10. 如图所示的是天安门周围的景点分布示意图.若以正东、正北方向为x轴、y轴的正方向建立坐标系,表示电报大楼的点的坐标为(-4,0),表示王府井的点的坐标为(3,2),则表示博物馆的点的坐标为( )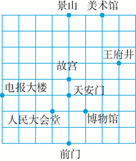 A、(1,0) B、(2,0) C、(1,-2) D、(1,-1)11. 如图,在平面直角坐标系中,点B,C,E,在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
A、(1,0) B、(2,0) C、(1,-2) D、(1,-1)11. 如图,在平面直角坐标系中,点B,C,E,在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )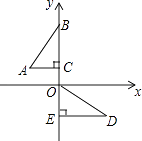 A、△ABC绕点C顺时针旋转90°,再向下平移3 B、△ABC绕点C顺时针旋转90°,再向下平移1 C、△ABC绕点C逆时针旋转90°,再向下平移1 D、△ABC绕点C逆时针旋转90°,再向下平移312. 如图,一个圆桶,底面直径为16cm,高为18cm,则一只小虫从下底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )
A、△ABC绕点C顺时针旋转90°,再向下平移3 B、△ABC绕点C顺时针旋转90°,再向下平移1 C、△ABC绕点C逆时针旋转90°,再向下平移1 D、△ABC绕点C逆时针旋转90°,再向下平移312. 如图,一个圆桶,底面直径为16cm,高为18cm,则一只小虫从下底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )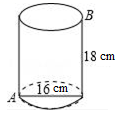 A、50cm B、40cm C、30cm D、20cm13. 下列各曲线中表示y是x的函数的是( )A、
A、50cm B、40cm C、30cm D、20cm13. 下列各曲线中表示y是x的函数的是( )A、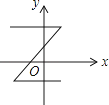 B、
B、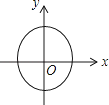 C、
C、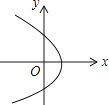 D、
D、 14. 正比例函数y=kx与一次函数y=x﹣k在同一坐标系中的图象大致应为( )A、
14. 正比例函数y=kx与一次函数y=x﹣k在同一坐标系中的图象大致应为( )A、 B、
B、 C、
C、 D、
D、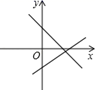 15. 如图图中,不能用来证明勾股定理的是( )A、
15. 如图图中,不能用来证明勾股定理的是( )A、 B、
B、 C、
C、 D、
D、 16. 在平面直角坐标系中,已知直线y=﹣ x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )A、(0,﹣ ) B、(0, ) C、(0,3) D、(0,4)
16. 在平面直角坐标系中,已知直线y=﹣ x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )A、(0,﹣ ) B、(0, ) C、(0,3) D、(0,4)二、填空题
-
17. 4是 的算术平方根.18. 如图x在数轴上表示数的点的位置,则化简|3x+ |的结果是 .
 19. 在平面直角坐标系中,点M(a-3,a+4),点N(5,9),若MN∥y轴,则a=.20. 如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是 .
19. 在平面直角坐标系中,点M(a-3,a+4),点N(5,9),若MN∥y轴,则a=.20. 如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是 .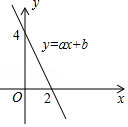
三、解答题
-
21. 计算:(1)、(2)、22.(1)、先化简,再求值: ,其中 .(2)、已知 , ,求下列式子的值:23. 如图, 中, , , ,将 折叠,使点B恰好落在斜边AC上,与点 重合,AD为折痕,求 的长.
 24. 如图, , ,点 在 轴上,且 .
24. 如图, , ,点 在 轴上,且 . (1)、求点 的坐标;(2)、求 的面积;(3)、在 轴上是否存在点 ,使以 、 、 三点为顶点的三角形的面积为10?若存在,请直接写出点 的坐标.若不存在,请说明理由.25. 已知 与x成正比,当 时,
(1)、求点 的坐标;(2)、求 的面积;(3)、在 轴上是否存在点 ,使以 、 、 三点为顶点的三角形的面积为10?若存在,请直接写出点 的坐标.若不存在,请说明理由.25. 已知 与x成正比,当 时,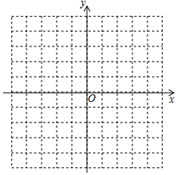 (1)、求y与x之间的函数关系式,在下列坐标系中画出函数图象;(2)、当 时,求函数y的值;(3)、结合图象和函数的增减性,求当 时自变量x的取值范围.26. 某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).(1)、分别写出两种优惠方法购买费用 (元 与所买水性笔支数 (支 之间的函数关系式;(2)、对 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;(3)、小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.
(1)、求y与x之间的函数关系式,在下列坐标系中画出函数图象;(2)、当 时,求函数y的值;(3)、结合图象和函数的增减性,求当 时自变量x的取值范围.26. 某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).(1)、分别写出两种优惠方法购买费用 (元 与所买水性笔支数 (支 之间的函数关系式;(2)、对 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;(3)、小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.