江苏省无锡市南长实验、侨谊教育集团2021届九年级上学期数学期中联考试卷

试卷更新日期：2020-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程为一元二次方程的是（）

A、x²－2＝0 B、ax²－2x－3=0 C、x²+y=1 D、x²－ $\frac{1}{x}$ －1＝0

查看试题解析
2. 已知关于x的一元二次方程(m－1)x²＋2x＋1＝0有实数根，则m的取值范围是（）

A、m＜2 B、m≤2 C、m＜2且m≠1 D、m≤2且m≠1

查看试题解析
3. 某企业2018年初获利润300万元，到2020年初计划利润达到507万元.设这两年的年利润平均增长率为x.应列方程是（）

A、300（1+x）=507 B、300（1+x）²=507 C、300（1+x）+300（1+x）²=507 D、300+300（1+x）+300（1+x）²=507

查看试题解析
4. 若等腰三角形的两条边长分别是方程x²-7x+10=0的两根，则等腰三角形的周长为（）

A、9 B、10 C、12 D、9或12

查看试题解析
5. 已知⊙O的半径为1，AO=d，且关于x的方程x²-2d x+1=0有两个相等的实数根，则点A与⊙O的位置关系是（）

A、在⊙O内 B、在⊙O外 C、在⊙O上 D、无法确定

查看试题解析
6. 下列语句中，正确的是（）

A、经过三点一定可以作圆 B、等弧所对的圆周角相等 C、相等的弦所对的圆心角相等 D、三角形的外心到三角形各边距离相等

查看试题解析
7. 正十边形的每一个外角的度数为（）

A、 $36 °$ B、 $30 °$ C、 $144 °$ D、 $150 °$

查看试题解析
8. 如图，菱形OABC的顶点A，B，C在⊙O上，过点B作⊙O的切线交OA的延长线于点D。若⊙O的半径为1，则BD的长为（）

A、1 B、2 C、 $\sqrt{2}$ D、 $\sqrt{3}$

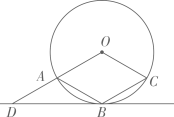查看试题解析
9. 如图，直线a⊥b，垂足为H，点P在直线b上，PH=4cm，O为直线b上一动点，以O为圆心1cm为半径作圆，当O从点P出发以2 cm/s速度向右作匀速运动，经过t s与直线a相切，则t为（）

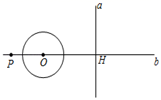A、2s B、 $\frac{3}{2}$ s或2s C、2s或 $\frac{5}{2}$ s D、 $\frac{3}{2}$ s或 $\frac{5}{2}$ s

查看试题解析
10. 如图，AB为半圆O的直径，M，C是半圆上的三等分点，AB＝8，BD与半圆O相切于点B.点P为 $\overset{⌢}{A M}$ 上一动点（A，M重合），直线PC交BD于点D，BE⊥OC于点E，延长BE交PC于点F，则下列结论正确的是：①PB＝PD；② $\overset{⌢}{B C}$ 的长为 $\frac{4}{3}$ π；③∠DBE＝45°；④当P为 $\overset{⌢}{A M}$ 中点时EC=EF；⑤∠DFB＝∠CBP.其中正确的个数为（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

11. 若关于x的一元二次方程x²-kx-2＝0的一个根为 $x = 1$ ，则k=.

查看试题解析
12. 设x₁ ， x₂是方程x²﹣3x﹣2=0的两个根，则代数式x₁²+x₂²的值为.

查看试题解析
13. 若关于x的一元二次方程x²+ax+3b＝0有一个根是3，则a+b的值为.

查看试题解析
14. 已知圆锥的底面半径为3cm，母线长为5cm，则这个圆锥的侧面积是cm².

查看试题解析
15. AB是半圆的直径，O为圆心，C是半圆上的点，D是 $\overset{⌢}{A C}$ 上的点，若∠BOC=50°，则∠D的度数为.

查看试题解析
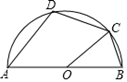16. 如图，AB是圆O的弦，半径OC⊥AB于点D，且OC=5cm，DC=2cm，则AB=.

查看试题解析
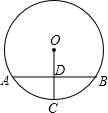17. 如图，在Rt△ABC中，∠C＝90°，AC＝BC，点O在AB上，经过点A的⊙O与BC相切于点D，交AB于点E，若 $C D = 2 \sqrt{2}$ ，则图中阴影部分面积为.

查看试题解析
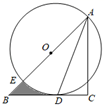18. 如图， AB是⊙O的直径，AB=2，∠ABC＝60°，P是⊙O上一动点，D是AP的中点，连接CD，则CD的最小值为.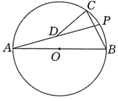

查看试题解析

三、解答题

19. 解方程：

(1)、（3x-1）²= （x+1）²

(2)、x²+10x-7=0 （用配方法）

(3)、x²+3x+1=0 （用公式法）

(4)、（x+5）（x-1）=7

查看试题解析
20. 如图，已知四边形ABCD是矩形，点E是CD的中点，

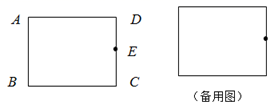(1)、画圆O，使该圆O过点A、B、E（保留作图痕迹）；

(2)、若AB=2，AD=3，则（1）中所画圆O的半径为.

查看试题解析
21. 已知关于x的一元二次方程x²+2x﹣k＝0有两个不相等的实数根.

(1)、求k的取值范围；

(2)、若方程的两个不相等的实数根是a，b，求 $\frac{1}{b + 1} - \frac{a}{a + 1}$ 的值.

查看试题解析
22. 如图，四边形ABCD内接于⊙O，AC平分∠BAD，延长DC交AB的延长线于点E．

(1)、若∠ADC=86°，求∠CBE的度数；

(2)、若AC=EC，求证：AD=BE

查看试题解析
23. 某景区商店以2元的批发价进了一批纪念品.经调查发现，每个定价3元，每天可以能卖出500件，而且定价每上涨0.1元，其销售量将减少10件.根据规定：纪念品售价不能超过批发价的2.5倍.

(1)、当每个纪念品定价为3.6元时，商店每天能卖出件；

(2)、如果商店要实现每天800元的销售利润，那该如何定价？

查看试题解析
24. 如图， $△ A B C$ 中， $∠ C = 90^{\circ}$ ， $A C = 8 c m$ ， $B C = 4 c m$ ，一动点P从点C出发沿着 $C B$ 方向以 $1 c m / s$ 的速度运动，另一动点Q从A出发沿着 $A C$ 边以 $2 c m / s$ 的速度运动，P，Q两点同时出发，运动时间为 $t (s)$ .

(1)、若 $△ P C Q$ 的面积是 $△ A B C$ 面积的 $\frac{1}{4}$ ，求t的值？

(2)、△PCQ的面积能否为 $△ A B C$ 面积的一半？若能，求出t的值；若不能，说明理由.

查看试题解析
25. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $C D$ 是斜边 $A B$ 上的中线，以 $C D$ 为直径的 $⊙ O$ 分别交 $A C$ 、 $B C$ 于点 $M$ 、 $N$ ，过点 $N$ 作 $N E ⊥ A B$ ，垂足为 $E$ ．

(1)、若 $⊙ O$ 的半径为 $\frac{5}{2}$ ， $A C = 6$ ，求 $B N$ 的长；

(2)、求证： $N E$ 与 $⊙ O$ 相切．

查看试题解析
26. 如图，⊙O为等边△ABC的外接圆，半径为2，点D在劣弧上运动（不与点A，B重合），连接DA，DB，DC.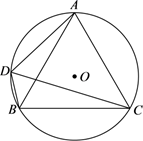

(1)、求证：DC是∠ADB的平分线；

(2)、设四边形ADBC的面积为S，线段DC的长为x，试用含x的代数式表示S；

(3)、若点M，N分别在线段CA，CB上运动（不含端点），经过探究发现，点D运动到每一个确定的位置，△DMN的周长有最小值t，随着点D的运动，t的值会发生变化，求所有t值中的最大值.

查看试题解析
27. 三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.

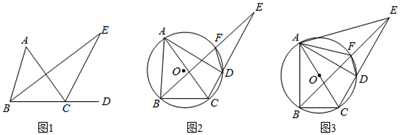(1)、如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，则∠E=.（请用含α的代数式表示）

(2)、如图2，四边形ABCD内接于⊙O， $\overset{⌢}{A D} = \overset{⌢}{B D}$ ，四边形ABCD的外角平分线DF交⊙O于点F，连结BF并延长交CD的延长线于点E.求证：∠BEC是△ABC中∠BAC的遥望角.

(3)、如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径.求∠AED的度数.

查看试题解析