江苏省苏州市新区一中2021届九年级上学期数学期中联考试卷
试卷更新日期:2020-12-09 类型:期中考试
一、单选题
-
1. 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为( )A、3 B、 C、 D、2. 方程x2=x的解是( )A、x=1 B、x1=﹣1,x2=1 C、x1=0,x2=1 D、x=03. 若正多边形的内角和是540°,则该正多边形的一个外角为( )
A、45° B、60° C、72° D、90°4. 平面内有一点P到圆上最远的距离是 ,最近的距离是 ,则圆的半径是( )A、 B、 C、 或 D、5. 在半径为2的圆中,弦AB的长为2,则 的长等于( )A、 B、 C、 D、6. 如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( ) A、8 B、4 C、10 D、57. 如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为( )
A、8 B、4 C、10 D、57. 如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为( )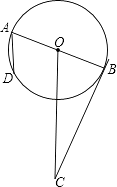 A、 B、 C、 D、8. 如图,矩形OCDE内接于扇形AOB,若点C是OA的中点,则∠BAD等于( )
A、 B、 C、 D、8. 如图,矩形OCDE内接于扇形AOB,若点C是OA的中点,则∠BAD等于( ) A、15°° B、18° C、22.5° D、30°9. 如图,已知第一象限内的点A在反比例函数 的图象上,第二象限的点B在反比例函数 的图象上,且OA⊥OB,tanA=2,则k的值为( )
A、15°° B、18° C、22.5° D、30°9. 如图,已知第一象限内的点A在反比例函数 的图象上,第二象限的点B在反比例函数 的图象上,且OA⊥OB,tanA=2,则k的值为( ) A、4 B、8 C、-4 D、-810. 如图, 与x轴交于点 , ,与 轴的正半轴交于点 .若 ,则点 的纵坐标为( )
A、4 B、8 C、-4 D、-810. 如图, 与x轴交于点 , ,与 轴的正半轴交于点 .若 ,则点 的纵坐标为( )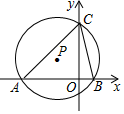 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知a是关于x方程 的一个根,则 的值为.12. 一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为 .13. 小明用一张扇形纸片做一个圆锥的侧面,已知该扇形的半径是10cm,弧长是12πcm2 , 那么这个圆锥的高是cm.14. 一元二次方程 的两根为x1 , x2 , 则 的值为.15. 如图,点A,B,D在⊙O上,∠A=20°,BC是⊙O的切线,B为切点,OD的延长线交BC于点C,则∠OCB=度.
 16. 如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为.
16. 如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为. 17. 如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从B点出发顺时针运动到D点时,点F经过的路径长为.
17. 如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从B点出发顺时针运动到D点时,点F经过的路径长为. 18. 如图,在平面直角坐标系中,已知C(6,8),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为.
18. 如图,在平面直角坐标系中,已知C(6,8),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为.

三、解答题
-
19. 计算题(1)、(2)、20. 解方程:(1)、3(x﹣2)2=x(x﹣2);(2)、3x2﹣6x+1=0(用配方法).21. 山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:(1)、每千克核桃应降价多少元?(2)、在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?22. 如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方 米处的点C出发,沿斜面坡度 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ .计算结果保留根号)
 23. 如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
23. 如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. (1)、求证:DE是⊙O的切线;(2)、若DE=6,AE=2 ,求⊙O的半径;(3)、在第(2)小题的条件下,求图中阴影部分的面积.24. 某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).
(1)、求证:DE是⊙O的切线;(2)、若DE=6,AE=2 ,求⊙O的半径;(3)、在第(2)小题的条件下,求图中阴影部分的面积.24. 某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号). 25. 如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.
25. 如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.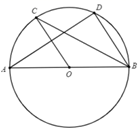 (1)、求证: ;(2)、若CE=2,EB=6,求⊙O的半径.26. 在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以原点O为圆心,半径为3的⊙O上,连接OC,过点O作OD⊥OC,OD与⊙O相交于点D(其中点C,O,D按逆时针方向排列),连接AB.
(1)、求证: ;(2)、若CE=2,EB=6,求⊙O的半径.26. 在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以原点O为圆心,半径为3的⊙O上,连接OC,过点O作OD⊥OC,OD与⊙O相交于点D(其中点C,O,D按逆时针方向排列),连接AB.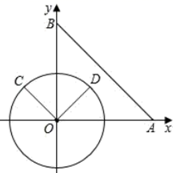 (1)、当OC//AB时,∠BOC的度数为.(2)、连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的最大值.(3)、连接AD,当OC//AD,点C位于第二象限时,
(1)、当OC//AB时,∠BOC的度数为.(2)、连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的最大值.(3)、连接AD,当OC//AD,点C位于第二象限时,①求出点C的坐标;
②直线BC是否为⊙O的切线?并说明理由.
27. 已知在平面直角坐标系xOy中,直线l1分别交x轴和y轴于点A(﹣3,0),B(0,3). (1)、如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长;(2)、如图2,已知直线l2:y=3x﹣3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心,2 为半径画圆.
(1)、如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长;(2)、如图2,已知直线l2:y=3x﹣3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心,2 为半径画圆.①当点Q与点C重合时,求证:直线l1与⊙Q相切;
②设⊙Q与直线l1相交于M,N两点,连结QM,QN.问:是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标;若不存在,请说明理由.