江苏省苏州市姑苏区五校联考2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-12-09 类型:期中考试
一、单选题
-
1. 下面的函数是二次函数的是( )A、 B、 C、 D、2. 若二次函数y=2x2的图象经过点P(1,a),则a的值为( )A、 B、1 C、2 D、43. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根4. 把二次函数 配方化为 形式是( ).A、 B、 C、 D、5. 在平面直角坐标系中,抛物线 经过变换后得到抛物线 ,则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移8个单位 D、向右平移8个单位6. 已知二次函数 中,其函数y与自变量x之间的部分对应值如下表所示:
x
…
0
1
2
3
4
…
y
…
4
1
0
1
4
…
点 、 在函数的图象上,则当1<x1<2,3<x2<4时, 与 的大小关系正确的是( )
A、 B、 C、 D、7. 我们知道方程x2+2x-3=0的解是x1=1,x2=-3,现给出另一个方程(2x+3)2+2(2x+3)-3=0,它的解是( ).A、x1=1,x2=3 B、x1=1,x2=-3 C、x1=-1,x2=3 D、x1=-1,x2=-38.已知函数y=(x﹣a)(x﹣b)(其中a>b)的图象如下面右图所示,则函数y=ax+b的图象可能正确的是( )
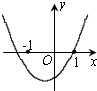 A、
A、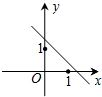 B、
B、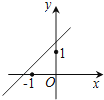 C、
C、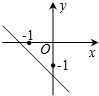 D、
D、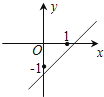 9. 当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为( )A、 或2 B、 或 C、2或 D、2或10. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
9. 当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为( )A、 或2 B、 或 C、2或 D、2或10. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、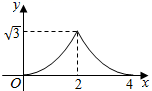 B、
B、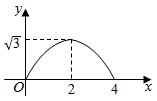 C、
C、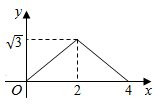 D、
D、
二、填空题
-
11. 关于x的方程ax2-3x-6=0是一元二次方程,则a满足的条件是.12. 方程(x﹣1)(x﹣3)=0的解为 .13. 若x1 , x2是方程 的两个实数根,则代数式 的值等于.14. 一个三角形的两边长分别为3和5,第三边长是方程x2-6x+8=0的根,则三角形的周长为.15. 科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃
-4
-2
0
1
4
植物高度增长量l/mm
41
49
49
46
25
科学家经过猜想、推测出l与t之间是二次函数关系.由此可以推测最适合这种植物生长的温度为℃.
16. 某型号的手机连续两次降价,单价由原来的5200元降到了1300元.设平均每次降价的百分率为x,则可以列出的一元二次方程是.17. 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的是(只填序号).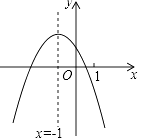 18. 如图,已知二次函数 的图象交x轴于A(-1,0),B(4,0),交y轴于点C,点P是直线BC上方抛物线上一动点(不与B,C重合),过点P作PE⊥BC,PF∥y轴交BC与F,则△PEF面积的最大值是.
18. 如图,已知二次函数 的图象交x轴于A(-1,0),B(4,0),交y轴于点C,点P是直线BC上方抛物线上一动点(不与B,C重合),过点P作PE⊥BC,PF∥y轴交BC与F,则△PEF面积的最大值是.
三、解答题
-
19. 解方程(1)、(2)、(3)、(4)、20. 已知关于x的方程3x2+mx-8=0.(1)、求证:不论m为何值,方程总有两个不相等的实数根;(2)、若方程有一个根是 ,求另一个根及m的值.21. 如图,要利用一面墙(墙长为25米)建一个矩形场地,用100米的围栏围成三个大小相同的矩形,设矩形的边长AB为x米,矩形场地的总面积为y平方米.
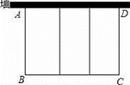 (1)、请用含有x的式子表示y(不要求写出x的取值范围);(2)、当x为何值时,矩形场地的总面积为400平方米?22. 已知关于x的一元二次方程x2﹣2x﹣a=0.
(1)、请用含有x的式子表示y(不要求写出x的取值范围);(2)、当x为何值时,矩形场地的总面积为400平方米?22. 已知关于x的一元二次方程x2﹣2x﹣a=0.
(1)、如果此方程有两个不相等的实数根,求a的取值范围;(2)、如果此方程的两个实数根为x1 , x2 , 且满足 ,求a的值.23. 某文具店购进一批纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的销售单价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.(1)、请求出y与x的函数关系式 ;(2)、写出该文具店每周销售这种纪念册所获得的利润为w元与销售单价x (元)的函数关系式;并确定当销售单价x为何值时,利润最大?(3)、试通过(2)中的函数关系式及其大致图象,帮助该文具店确定产品的销售单价范围,使利润不低于150元(请直接写出销售单价x的范围).24. 在平面直角坐标系xOy中,直线 与x轴、y轴分别交于点A、B(如图).抛物线y=ax2+bx(a≠0)经过点A.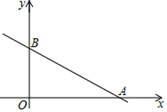 (1)、求线段AB的长;(2)、如果抛物线y=ax2+bx经过线段AB上的另一点C,且 ,求这条抛物线的表达式;(3)、如果抛物线y=ax2+bx的顶点D位于△AOB内,则a的取值范围是.25. 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(3,0),(3,4).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中点M沿OA 向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP,已知动点运动了x秒.
(1)、求线段AB的长;(2)、如果抛物线y=ax2+bx经过线段AB上的另一点C,且 ,求这条抛物线的表达式;(3)、如果抛物线y=ax2+bx的顶点D位于△AOB内,则a的取值范围是.25. 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(3,0),(3,4).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中点M沿OA 向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP,已知动点运动了x秒.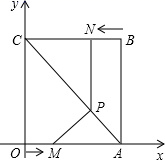 (1)、求点P的坐标(用含x的代数式表示).(2)、试求△MPA面积的最大值,并求此时x的值.(3)、请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的探索结果.26. 已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(1,0)、B(3,0)两点,与y轴交于C点(0,-3).
(1)、求点P的坐标(用含x的代数式表示).(2)、试求△MPA面积的最大值,并求此时x的值.(3)、请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的探索结果.26. 已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(1,0)、B(3,0)两点,与y轴交于C点(0,-3).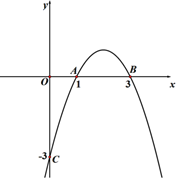 (1)、求a的值;(2)、若P为二次函数y=ax2+bx+c(a≠0)图象的顶点,求证:∠ACO=∠PCB;(3)、若Q为二次函数y=ax2+bx+c(a≠0)图象上一点,且∠ACO=∠QCB,求Q点的坐标.27. 如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)、求a的值;(2)、若P为二次函数y=ax2+bx+c(a≠0)图象的顶点,求证:∠ACO=∠PCB;(3)、若Q为二次函数y=ax2+bx+c(a≠0)图象上一点,且∠ACO=∠QCB,求Q点的坐标.27. 如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.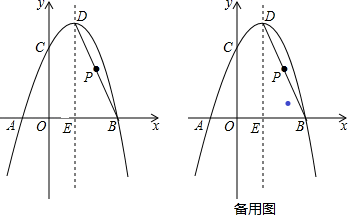 (1)、求经过A,B,C三点的抛物线的函数表达式;(2)、点Q在该抛物线的对称轴上,若△BCQ是以BC为直角边的直角三角形,求点Q的坐标;(3)、若P为BD的中点,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、N、G为顶点的四边形是正方形时,请求出点M的坐标.
(1)、求经过A,B,C三点的抛物线的函数表达式;(2)、点Q在该抛物线的对称轴上,若△BCQ是以BC为直角边的直角三角形,求点Q的坐标;(3)、若P为BD的中点,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、N、G为顶点的四边形是正方形时,请求出点M的坐标.