江苏省泗阳县2021届九年级上学期数学期中联考试卷
试卷更新日期：2020-12-09 类型：期中考试
一、单选题
-
1. 一元二次方程x2=4x的解是（ ）A、x=4 B、x=0 C、x=0或-4 D、x=0或42. 的半径为5，圆心O到直线l的距离为3，则直线l与 的位置关系是A、相交 B、相切 C、相离 D、无法确定3. 一元二次方程 的根的情况是（ ）A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断方程根的情况4. 如图，AB是⊙O的直径，若∠BAC=420 ， 则么∠ABC=（ ）
A、420 B、480 C、580 D、5205. 已知x1、x2是一元二次方程x2-5x+6=0的两个实数根，则x1+x2=（ ）A、5 B、6 C、-5 D、-66. 小明不慎把家里的圆形镜子打碎了，其中三块碎片如图所示，三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是（ ）
A、① B、② C、③ D、均不可能7. 如图，四边形ABCD内接于⊙O ， 若∠BCD＝110°，则∠BOD的度数为（ ）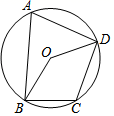
A、35° B、70° C、110° D、140°8. 如图，已知⊙O是△ABC的内切圆，且∠ABC=50°，∠ACB=80°.则∠BOC等于（ ）
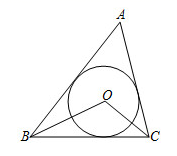A、125° B、120° C、115° D、100°9. 如图，如果从半径为6cm的圆形纸片剪去 圆周的一个扇形，将留下的扇形围成一个圆锥(接缝处不重叠)，那么这个圆锥的底面半径为（ ）
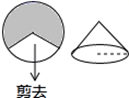A、2cm B、4cm C、6cm D、8cm10. 如图，点C是以AB为直径的圆上一个动点（不与点A、B重合），且AC+BC=12.若AB=m（m为整数），则整数m的值的个数为（ ）
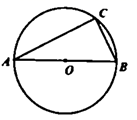A、0个 B、2个 C、3个 D、4个二、填空题
-
11. 关于x的方程kx2+2x+1=0是一元二次方程，则k应满足的条件是.12. 已知a是关于x方程x2-2x-8=0的一个根，则a2-2a的值为.13. 直角三角形的两直角边长分别为6和8，它的外接圆的半径是.14. 如图，在矩形ABCD中， AB=3， AD=4，若以点 A为圆心，以 4为半径作 ⊙A，则点 A，点B，点 C，点 D四点中在 ⊙A外的是.
15. 如图，AB为⊙O的直径，C是BA延长线上一点，点D在⊙O上，且CD=OA，CD的延长线交⊙O于点E，若∠C=23°，则∠EOB的度数为.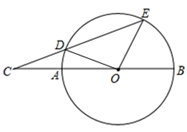
16. 如图，AB是⊙O的直径，点D在AB的延长线上，过点D作⊙O的切线，切点为C，若∠A=25°，则∠D=.
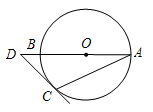17. 如图，正六边形ABCDEF的边长为2，以点B为圆心，AB长为半径，作扇形ABC，则图中阴影部分的面积为.
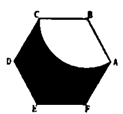18. 如图，△ABC为等边三角形，AC=8，D在线段AB上，AD=2，以D为圆心，AD为半径画圆，点E为OD上的一动点，连接CE，将线段CE绕点C逆时针旋转60°得到CF，连接AF、BF.则△ABF面积的最大值为.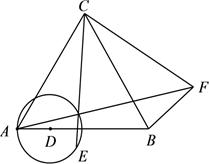
三、解答题
-
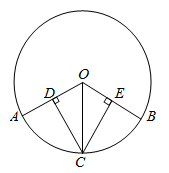
19. 解下列方程(1)、（x+2）2-16=0(2)、2x2-5x+2=020. 如图： ，CD⊥OA于D，CE⊥OB于E，求证：CD=CE.
21. 已知，关于x的一元二次方程x2-2mx+m2-1=0(1)、不解方程，判别方程的根的情况.(2)、若x=1是方程的一个根，请求出m的值.22. 如图，正方形ABCD内接于⊙O，M为弧CD的中点，连接AM，BM，求证：AM＝BM.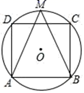
23. 实践操作如图，△ABC是直角三角形，∠ACB=90°，利用直尺和圆规按下列要求作图，并在图中标明相应的字母.（保留作图痕迹，不写作法）
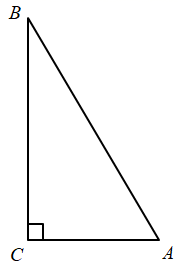
（ 1 ）作∠BAC的平分线，交BC于点O.
（ 2 ）以O为圆心，OC为半径作圆.
综合运用
在你所作的图中，直线AB与⊙O存在怎样的位置关系，请说明理由.
24. 如图，已知△ABC是⊙O的内接三角形，AD是⊙O的直径，连结BD，BC平分∠ABD.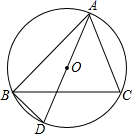
(1)、求证：∠CAD=∠ABC；(2)、若AD=6，求 的长.25. 为抗击新型肺炎疫情，某服装厂及时引进了一条口罩生产线生产口罩，开工第一天生产10万件，第三天生产14.4万件，若每天增长的百分率相同.试回答下列问题：(1)、求每天增长的百分率；(2)、经调查发现，1条生产线最大产能是20万件/天，若每增加1条生产线，每条生产线的最大产能将减少2万件/天，现该厂要保证每天生产口罩60万件，在增加产能同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？26. 如图，AB为⊙O的直径，C为⊙O上一点，∠ABC的角平分线交⊙O于点D.过点D作DE⊥BC，交BC的延长线于点E.
(1)、试判断DE与⊙O的位置关系，并说明理由.(2)、过点D作DF⊥AB于点F，连接CD，若CD=2，BD=2 ，求图中阴影部分的面积.27. 如图l，在矩形ABCD中，AB=6cm，BC=8cm，点P从点B出发，沿AB边向终点A以每秒1cm的速度运动，同时点Q从点C出发沿C→B→A向终点A以每秒3cm的速度运动，P、Q其中一点到达终点时，另一点随之停止运动，设运动时间为t秒.解答下列问题：
(1)、当Q在BC边时，①当t为 ▲ 秒时，PQ的长为2 cm？
②连接AQ，当t为几秒时，△APQ的面积等于16cm2？
(2)、如图2，以P为圆心，PQ长为半径作⊙P，在整个运动过程中，是否存在这样的t值，使⊙P正好与△ABD的一边（或边所在的直线）相切？若存在，求出t值；若不存在，请说明理由.28. 如图1，AB是⊙O的一条弦，点C是 上一点.
(1)、若∠ACB=30°，AB=4.求⊙O的半径.(2)、如图2，若点P是⊙O外一点.点P、点C在弦AB的同侧.连接PA、PB.比较∠APB与∠ACB的大小关系，并说明理由.(3)、如图3.设点G为AC的中点，在 上取一点D.使得 ，延长BA至E，使AE=AB，连接DE，F为DE的中点，过点A作BE的垂线，交⊙O于点P，连接PF，PG.写出PG与PF的数量关系，并说明理由.