北京市海淀区西三旗2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2020-12-09 类型:期中考试
一、单选题
-
1. 下列四个图形,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 点 关于x轴对称的点的坐标为( )A、 B、 C、 D、3. 如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
2. 点 关于x轴对称的点的坐标为( )A、 B、 C、 D、3. 如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )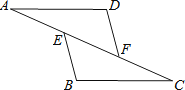 A、∠A=∠C B、∠D=∠B C、AD∥BC D、DF∥BE4. 下列计算中正确的是( )A、2x+3y=5xy B、x·x4=x4 C、 D、5. 若一个正多边形的每一个内角为156°,则这个正多边形的边数是( )A、14 B、15 C、16 D、176. 如果等腰三角形的两边长是10cm和5cm,那么它的周长为( )A、20cm B、25cm C、20cm或25cm D、15cm7. AD是△ABC的角平分线,过点D作DE⊥AB于E,DF⊥AC于F,则下列结论不一定正确的是( )A、DE=DF B、BD=CD C、AE=AF D、∠ADE=∠ADF8. 如图所示,把一个正方形对折两次后沿虚线剪下,展开后所得的图形是( )
A、∠A=∠C B、∠D=∠B C、AD∥BC D、DF∥BE4. 下列计算中正确的是( )A、2x+3y=5xy B、x·x4=x4 C、 D、5. 若一个正多边形的每一个内角为156°,则这个正多边形的边数是( )A、14 B、15 C、16 D、176. 如果等腰三角形的两边长是10cm和5cm,那么它的周长为( )A、20cm B、25cm C、20cm或25cm D、15cm7. AD是△ABC的角平分线,过点D作DE⊥AB于E,DF⊥AC于F,则下列结论不一定正确的是( )A、DE=DF B、BD=CD C、AE=AF D、∠ADE=∠ADF8. 如图所示,把一个正方形对折两次后沿虚线剪下,展开后所得的图形是( )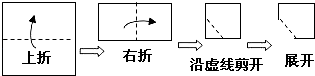 A、
A、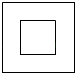 B、
B、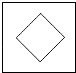 C、
C、 D、
D、 9. 如图,△ABC中,若AB=AC , BD=CE , CD=BF , 则∠EDF=( )
9. 如图,△ABC中,若AB=AC , BD=CE , CD=BF , 则∠EDF=( )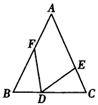 A、90°-∠A B、180°-2∠A C、 D、10. 如图,三角形的顶点落在折叠后的四边形内部,则∠γ与∠α+∠β之间的关系是( )
A、90°-∠A B、180°-2∠A C、 D、10. 如图,三角形的顶点落在折叠后的四边形内部,则∠γ与∠α+∠β之间的关系是( ) A、∠γ=∠α+∠β B、2∠γ=∠α+∠β C、3∠γ=2∠α+∠β D、3∠γ=2(α∠+∠β)
A、∠γ=∠α+∠β B、2∠γ=∠α+∠β C、3∠γ=2∠α+∠β D、3∠γ=2(α∠+∠β)二、填空题
-
11. 等腰三角形是对称图形,它至少有 条对称轴.12. 计算: ;13. 已知点A(a , 2)和B(﹣3,b),点A和点B关于y轴对称,则a+b= .14. 在△ABC和△ 中,若∠A=∠ ,AB= ,请你补充一个条件 , 使得△ABC ≌△ .15. 等腰三角形的一个外角是110°,它的顶角的度数是 .16. 在 中, , , 垂直平分 交BC于D,垂足为E,若 ,则 .
 17. 如图,在ΔABC中,∠ABC=120°,点D、E分别在AC和AB上,且AE=ED=DB=BC,则∠A的度数为°.
17. 如图,在ΔABC中,∠ABC=120°,点D、E分别在AC和AB上,且AE=ED=DB=BC,则∠A的度数为°. 18. 一组按一定规律排列的式子: ,…,(a≠0)则第n个式子是
18. 一组按一定规律排列的式子: ,…,(a≠0)则第n个式子是三、解答题
-
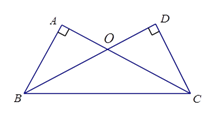
19. 计算:(1)、(2)、(3)、20. 如图,在△ABC和△DCB中,AB⊥AC ,CD⊥BD ,AB=DC , AC与BD交于点O . 求证:AC=BD .
 21. 在平面直角坐标系中的位置如图所示.
21. 在平面直角坐标系中的位置如图所示. (1)、作出 关于y轴对称的 ,并写出 顶点 的坐标;(2)、 的面积等于 .22. 计算:(1)、先化简,再求值: ,其中 ;(2)、已知 ,求 的值.23. 已知:如图,四边形ABCD中,∠A=∠B=90°,∠C=60°,CD=2AD,AB=4.
(1)、作出 关于y轴对称的 ,并写出 顶点 的坐标;(2)、 的面积等于 .22. 计算:(1)、先化简,再求值: ,其中 ;(2)、已知 ,求 的值.23. 已知:如图,四边形ABCD中,∠A=∠B=90°,∠C=60°,CD=2AD,AB=4.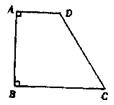 (1)、在AB边上求作点P,使PC+PD最小:(2)、求出(1)中PC+PD的最小值.24. 如图, 为等边三角形,点D为BC延长线上的一点,射线CM平分∠ACD , E是CM上一点,且CE=BD , 连接AD、AE、DE .
(1)、在AB边上求作点P,使PC+PD最小:(2)、求出(1)中PC+PD的最小值.24. 如图, 为等边三角形,点D为BC延长线上的一点,射线CM平分∠ACD , E是CM上一点,且CE=BD , 连接AD、AE、DE .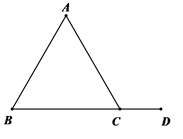 (1)、根据描述补全图形(角平分线无需尺规作图)(2)、试判断 的形状,并说明理由.25. 已知四边形ABCD中,AB⊥AD , BC⊥CD , AB=BC , ∠ABC=120゜,∠MBN=60゜,∠MBN绕B点旋转,它的两边分别交AD , DC(或它们的延长线)于E , F .
(1)、根据描述补全图形(角平分线无需尺规作图)(2)、试判断 的形状,并说明理由.25. 已知四边形ABCD中,AB⊥AD , BC⊥CD , AB=BC , ∠ABC=120゜,∠MBN=60゜,∠MBN绕B点旋转,它的两边分别交AD , DC(或它们的延长线)于E , F . (1)、当∠MBN绕B点旋转到AE=CF时(如图1),试猜想线段AE、CF、EF之间存在的数量关系为 . (不需要证明);(2)、当∠MBN绕B点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请写出你的猜想,不需证明.
(1)、当∠MBN绕B点旋转到AE=CF时(如图1),试猜想线段AE、CF、EF之间存在的数量关系为 . (不需要证明);(2)、当∠MBN绕B点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请写出你的猜想,不需证明.