江苏省苏州市吴中、吴江区2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2020-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列实数 $\frac{22}{7}$ ， $\sqrt{3}$ ， $\frac{π}{3}$ ，0.101001其中无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列各组数中互为相反数的一组是（）

A、2与 $\frac{1}{2}$ B、 $| - 2 |$ 与 $\sqrt{4}$ C、-2与 $\sqrt{{(- 2)}^{2}}$ D、2与 $\sqrt[3]{8}$

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $\sqrt{5} \times \sqrt{3} = \sqrt{15}$ C、 ${(2 \sqrt{2})}^{2} = 16$ D、 $\frac{3}{\sqrt{3}} = 1$

查看试题解析
5. 下列二次根式中，最简二次根式的是（）

A、 $\sqrt{\frac{1}{5}}$ B、 $\sqrt{0.5}$ C、 $\sqrt{5}$ D、 $\sqrt{50}$

查看试题解析
6. 等腰三角形的一个角是80°，则它的底角是（）

A、50° B、80° C、50°或80° D、20°或80°

查看试题解析
7. 下列关于 $\sqrt{5}$ 的说法中，错误的是（）

A、 $\sqrt{5}$ 是无理数 B、2< $\sqrt{5}$ <3 C、5的平方根是 $\sqrt{5}$ D、 $\sqrt{5}$ 是5的算术平方根

查看试题解析
8. 由下列条件不能判定△ABC为直角三角形的是（）

A、 $∠$ A十 $∠$ B= $∠$ C B、a=5，b=12，c=13 C、 $(c + b) (c - b) = a^{2}$ D、 $a = \frac{1}{3}$ ， $b = \frac{1}{4}$ ， $c = \frac{1}{5}$

查看试题解析
9. 如图，在 $Δ A B C$ 中， $∠ B A C = 108 °$ ，将 $Δ A B C$ 绕点A按逆时针方向旋转得到 $Δ A B^{'} C^{'}$ .若点 $B^{'}$ 恰好落在 $B C$ 边上，且 $A B^{'} = C B^{'}$ ，则 $∠ C^{'}$ 的度数为（）

A、 $18 °$ B、 $20 °$ C、 $24 °$ D、 $28 °$

查看试题解析
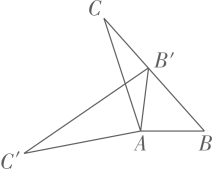10. 如图，AB=AD，AC=AE， $∠$ DAB= $∠$ CAE=50° ，以下四个结论：①△ADC≌△ABE；②CD=BE；③ $∠$ DOB=50°；④点A在 $∠$ DOE的平分线上，其中结论正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. -1 的立方根是

查看试题解析
12. 小亮的体重为43.85kg，精确到0.1kg所得近似值为kg.

查看试题解析
13. 使 $\sqrt{x - 2}$ 有意义的x的取值范围是．

查看试题解析
14. 若最简二次根式 $\sqrt{7 a - 1}$ 与 $\sqrt{6 a + 1}$ 是同类二次根式，则a= ．

查看试题解析
15. 等腰三角形的两边长分别为7cm和3cm，则它的周长为.

查看试题解析
16. 如图，在△ACB中， $∠$ C=90°，AB的垂直平分线交AB、AC于点M、N，若AC=8，BC=4，则NC的长度为.

查看试题解析
17. 一个正数的两个平方根为a+2和a-6，则这个数为.

查看试题解析
18. 如图，在四边形ABCD中，AB =AD，BC=DC，点E为AD边上一点，连接BD、CE，CE与BD交于点F，且CE∥AB，若 $∠$ A =60°，AB=4，CE=3，则BC的长为.

查看试题解析

三、解答题

19. 求下列各式中的x的值

(1)、 $x^{3} + 125 = 0$

(2)、 ${(x + 1)}^{2} - 25 = 0$

查看试题解析
20. 计算：

(1)、 $\sqrt[3]{{(- 1)}^{3}} + \sqrt{32} - | \sqrt{2} - 1 |$

(2)、 $(\sqrt{18} - \sqrt{8} + \sqrt{2}) \times \sqrt{6}$

查看试题解析
21.

(1)、若实数m、n满足等式 $| m - 2 | + \sqrt{n - 4} = 0$ ，求2m+3n的平方根；

(2)、已知 $y = \sqrt{x - 24} + \sqrt{24 - x} - 8$ ，求 $\sqrt[3]{x - 5 y}$ 的值.

查看试题解析
22. 如图，在边长为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上，

(1)、在图中画出与△ABC关于直线 $l$ 成轴对称的△A'B'C'；

(2)、四边形ABB'A'的周长为；

(3)、在直线 $l$ 上找一点P，使PA+PB的长最短，则这个最短长度为.

查看试题解析
23. 学完勾股定理之后，同学们想利用升旗的绳子、卷尺，测算出学校旗杆的高度.爱动脑筋的小明这样设计了一个方案：将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端5米处，发现此时绳子底端距离打结处约1米.请你设法帮小明算出旗杆的高度.

查看试题解析
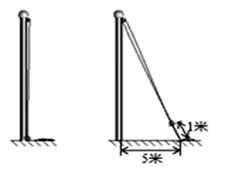24. 如图，在△ABC中， $∠$ ABC、 $∠$ ACB的平分线交于点O，过点O作EF//BC交AB于E，交AC于F.

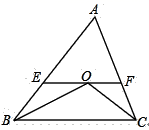(1)、求证：△EBO为等腰三角形；

(2)、若△AEF的周长为15，AB=8，求AC的长度.

查看试题解析
25. 如图，四边形ABCD中， $∠$ BAD= $∠$ BCD=90°，E为对角线BD的中点，连接AE、CE.

(1)、求证：AE=CE；

(2)、若AC=8，BD=10，求△ACE的面积.

查看试题解析
26. 像 $\sqrt{2} \cdot \sqrt{2} = 2$ ； $(\sqrt{3} + 1) \sqrt{3} - 1) = 2$ ； $(\sqrt{5} + \sqrt{2}) \sqrt{5} - \sqrt{2}) = 3$ ......两个含有二次根式的代数式相乘，积不含有二次根式，则称这两个代数式互为有理化因式.爱动脑筋的小明同学在进行二次根式计算时，利用有理化因式化去分母中的根号.
（ 1 ） $\frac{1}{2 \sqrt{3}} = \frac{\sqrt{3}}{2 \sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{6}$ ；

（ 2 ） $\frac{\sqrt{2} + 1}{\sqrt{2} - 1} = \frac{{(\sqrt{2} + 1)}^{2}}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = \frac{2 + 2 \sqrt{2} + 1}{2 - 1} = 3 + 2 \sqrt{2}$

勤奋好学的小明发现；可以用平方之后再开方的方式来化简一些有特点的无理数.

（ 3 ）化简： $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ .

解：设 $x = \sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ ，易知 $\sqrt{3 + \sqrt{5}} > \sqrt{3 - \sqrt{5}}$ ，则 $x > 0$ .

由： $x^{2} = 3 + \sqrt{5} + 3 - \sqrt{5} - 2 \sqrt{(3 + \sqrt{5}) (3 - \sqrt{5})} = 6 - 2 \sqrt{4} = 2$ .解得 $x = \sqrt{2}$ .

即 $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ = $\sqrt{2}$ .

请你解决下列问题：

(1)、 $2 \sqrt{3} - 3 \sqrt{5}$ 的有理化因式是；

(2)、化简： $\frac{3}{\sqrt{3}} + \frac{1}{\sqrt{2} - 1} + \frac{1}{2 + \sqrt{3}}$ ；

(3)、化简： $\sqrt{6 - 3 \sqrt{3}} - \sqrt{6 + 3 \sqrt{3}}$ .

查看试题解析
27. （探索发现）
如图①，已知在△ABC中， $∠$ BAC= 45°，AD $⊥$ BC，垂足为D，BE $⊥$ AC，垂足为E，AD与BE相交于F.

(1)、线段AF与BC的数量关系是：AFBC，（用>，<，=填空）；

(2)、若 $∠$ ABC=67.5°，试猜想线段AF与BD有何数量关系，并说明理由.

(3)、（拓展应用）
如图②，在△ABC中，AD $⊥$ BC，垂足为D，已知 $∠$ BAC=45°， $∠$ C=22.5°，AD= $2 \sqrt{2}$ ，求△ABC的面积.

查看试题解析
28. 某校机器人兴趣小组在如图所示的三角形场地上开展训练.已知：AB=10，BC=6，AC=8；机器人从点C出发，沿着△ABC边按C $\to$ B $\to$ A $\to$ C的方向匀速移动到点C停止；机器人移动速度为每秒2个单位，移动至拐角处调整方向需要1秒（即在B、A处拐弯时分别用时1秒）.设机器人所用时间为t秒时，其所在位置用点P表示（机器人大小不计）.

(1)、点C到AB边的距离是；

(2)、是否存在这样的时刻，使△PBC为等腰三角形？若存在，求出t的值；若不存在，请说明理由.

查看试题解析