江苏省南通市八一中学2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2020-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列倡导节约的图案中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 分式 $\frac{1}{x + 2}$ 有意义，x的取值范围是（）

A、x≠2 B、x≠﹣2 C、x＝2 D、x＝﹣2

查看试题解析
3. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a + 2 a^{2} = 3 a^{3}$ C、 $4 x^{3} \cdot 2 x = 8 x^{4}$ D、 ${(- 3 a^{2})}^{3} = - 9 a^{6}$

查看试题解析
4. 将多项式 $a^{2} - 6 a - 5$ 变为 ${(x + p)}^{2} + q$ 的形式，结果正确的是（）

A、 ${(a + 3)}^{2} - 14$ B、 ${(a - 3)}^{2} - 14$ C、 ${(a + 3)}^{2} + 4$ D、 ${(a - 3)}^{2} + 4$

查看试题解析
5. 如图，已知在△ABC，AB＝AC．若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是（）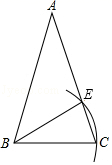

A、AE＝EC B、AE＝BE C、∠EBC＝∠BAC D、∠EBC＝∠ABE

查看试题解析
6. 已知 $a + b = 1$ ，则 $a^{2} - b^{2} + 2 b$ 的值为（）

A、0 B、1 C、3 D、4

查看试题解析
7. 已知a，b，c是△ABC的三边长，且满足 $a^{2} + c^{2} = 2 b (a + c - b)$ ，则此三角形是（）

A、等边三角形 B、等腰三角形 C、直角三角形 D、无法确定

查看试题解析
8. 如图，在△ABC中，AB＝AC，∠A＝120°，BC＝6 cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（）

A、4 cm B、3 cm C、2 cm D、1 cm

查看试题解析
9. 如图，将一块长方形纸片ABCD沿BD翻折后，点C与E重合，若∠ADE = 30°，EH = 2，则BC的长度为（）

A、8 B、7 C、6.5 D、6

查看试题解析
10. 如图，点C、D在线段AB的同侧，CA＝4，AB＝12，BD＝9，M是AB的中点，∠CMD＝120°，则CD长的最大值是（）

A、16 B、19 C、20 D、21

查看试题解析

二、填空题

11. 计算： ${(3 - π)}^{0} =$ .

查看试题解析
12. 若分式 $\frac{x - 1}{x}$ 的值为0，则 $x$ 的值为.

查看试题解析
13. 在平面直角坐标系xOy中，点C(3，－1)，则点C关于y轴对称点的坐标为.

查看试题解析
14. 一个等腰三角形两边的长分别为3和8，那么这个三角形的周长是．

查看试题解析
15. 若 $x - \frac{1}{x} = 1$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值是.

查看试题解析
16. 如图，以等边△ABC的边AC为腰作等腰△CAD ，使AC=AD ，连接BD ，若∠DBC=41°，∠CAD=°.

查看试题解析
17. 如图， $△$ ABC中，AD垂直BC于点D，且AD = BC，BC上方有一动点P满足 $S_{△ P B C} = \frac{1}{2} S_{△ A B C}$ ，则点P到B、C两点距离之和最小时，∠PBC的度数为.

查看试题解析
18. 若m²=n+2，n²=m+2（m≠n），则m³-2mn+n³的值为．

查看试题解析

三、解答题

19. 计算：

(1)、 $(m + n) (m - n) - n (2 m - n)$ ；

(2)、 $(3 m^{2} + 15 m^{3} n - m^{4}) \div (- 3 m^{2})$ .

查看试题解析
20. 因式分解：

(1)、 $x^{2} - y^{2}$ ；

(2)、 $a x^{2} + 4 a x + 4 a$ .

查看试题解析
21. 先化简，再求值 ${(x - 2 y)}^{2} - x (x + 3 y) - 4 y^{2}$ ，其中 $x = - 4 ， y = \frac{1}{2}$ .

查看试题解析
22. 如图所示，在平面直角坐标系中，A(－1，4)，B(－3，3)，C(－2，1).

(1)、已知 $△$ A₁B₁C₁与 $△$ ABC关于x轴对称，画出 $△$ A₁B₁C₁ ，并写出点A₁坐标：

(2)、在y轴上作出点P（在图中显示作图过程），使得PA+PC的值最小，并写出点P的坐标.

查看试题解析
23.

(1)、若 $2 x + 5 y - 3 = 0$ ，求 $4^{x} \cdot 32^{y}$ 的值；

(2)、若 $a^{2} + a b = 7 + m$ ， $b^{2} + a b = 9 - m$ ，求a+b的值.

查看试题解析
24. 如图，等腰Rt△ABC中，∠ACB = 90°，CA = CB，点D在AB上，AD = AC，BE⊥直线CD于E.

(1)、求∠BCD的度数；

(2)、求证：CD = 2BE；

(3)、若点O是AB的中点，请直接写出三条线段CB、BD、CO之间的数量关系.

查看试题解析
25. 阅读材料
小明遇到这样一个问题：求计算 $(x + 2) (2 x + 3) (3 x + 4)$ 所得多项式的一次项系数.

小明想通过计算 $(x + 2) (2 x + 3) (3 x + 4)$ 所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法.

他决定从简单情况开始，先找 $(x + 2) (2 x + 3)$ 所得多项式中的一次项系数，通过观察发现：

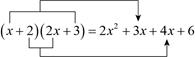
也就是说，只需用 $x + 2$ 中的一次项系数1乘以 $2 x + 3$ 中的常数项3，再用 $x + 2$ 中的常数项2乘以 $2 x + 3$ 中的一次项系数2，两个积相加 $1 \times 3 + 2 \times 2 = 7$ ，即可得到一次项系数.

延续上面的方法，求计算 $(x + 2) (2 x + 3) (3 x + 4)$ 所得多项式的一次项系数，可以先用 $x + 2$ 的一次项系数1， $2 x + 3$ 的常数项3， $3 x + 4$ 的常数项4，相乘得到12；再用 $2 x + 3$ 的一次项系数2， $x + 2$ 的常数项2， $3 x + 4$ 的常数项4，相乘得到16；然后用 $3 x + 4$ 的一次项系数3， $x + 2$ 的常数项2 $2 x + 3$ 的常数项3，相乘得到18.最后将12，16，18相加，得到的一次项系数为46.

参考小明思考问题的方法，解决下列问题：

(1)、计算 $(x + 4) (4 x + 3)$ 所得多项式的一次项系数为.

(2)、计算 $(x + 1) (3 x - 2) (2 x + 5)$ 所得多项式的一次项系数为.

(3)、若 $x^{2} - 3 x + 1$ 是 $x^{4} + a x^{2} + b x + 2$ 的一个因式，求 $a$ 、 $b$ 的值.

查看试题解析
26. 在平面直角坐标系xOy中，我们称横纵坐标都是整数的点为整点.若坐标系内两个整点A(p，q)、B(m，n)(m≤n)满足关于x的多项式 $x^{2} + p x + q$ 能够因式分解为 $(x + m) (x + n)$ ，则称点B是A的分解点.例如A(3，2)、B(1，2)满足 $x^{2} + 3 x + 2 = (x + 1) (x + 2)$ ，所以B是A的分解点.

(1)、在点A₁(5，6)、A₂(0，3)、A₃(－2，0)中，请找出不存在分解点的点；

(2)、点P、Q在纵轴上（P在Q的上方），点R在横轴正半轴上，且点P、Q、R都存在分解点，若 $△$ PQR面积为6，请直接写出满足条件的 $△$ PQR的个数及每个三角形的顶点坐标；

(3)、已知点D在第一象限内，D是C的分解点，请探究 $△$ OCD是否可能是等腰三角形？若可能，请求出所有满足条件的点D的坐标；若不可能，请说明理由.

查看试题解析