初中数学苏科版2020-2021学年九年级上学期期末模拟测试
试卷更新日期:2020-12-09 类型:期末考试
一、单选题
-
1. 若关于x的方程x2+x-a+=0 有两个不相等的实数根,则实数a的取值范围是( )A、
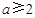 B、
B、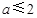 C、a>2
D、
C、a>2
D、 2. 关于x的一元二次方程 的两根 , ,则 的值是( ).A、4 B、8 C、12 D、103. 如图,以AB为直径的半圆上有一点C,∠C=25°, 则的度数为( )
2. 关于x的一元二次方程 的两根 , ,则 的值是( ).A、4 B、8 C、12 D、103. 如图,以AB为直径的半圆上有一点C,∠C=25°, 则的度数为( )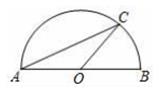 A、25° B、30° C、50° D、65°4. 如图,已知直线 与x轴、y轴分别交于B,C两点,点A是以D(0,2)为圆心,2为半径的⊙D上的一个动点,连接AC、AB,则△ABC面积的最小值是( )
A、25° B、30° C、50° D、65°4. 如图,已知直线 与x轴、y轴分别交于B,C两点,点A是以D(0,2)为圆心,2为半径的⊙D上的一个动点,连接AC、AB,则△ABC面积的最小值是( ) A、30 B、29 C、28 D、275. 某校足球队有16名队员,队员的年龄情况统计如下:
A、30 B、29 C、28 D、275. 某校足球队有16名队员,队员的年龄情况统计如下:年龄/岁
13
14
15
16
人数
3
5
6
2
则这16名队员年龄的中位数和众数分别是( )
A、14,15 B、15,15 C、14.5,14 D、14.5,156. 在市运动会射击比赛选拔赛中,某校射击队甲、乙、丙、丁四名队员的10次射击成绩如图所示.他们的平均成绩均是9.0环,若选一名射击成绩稳定的队员参加比赛,最合适的人选是( )
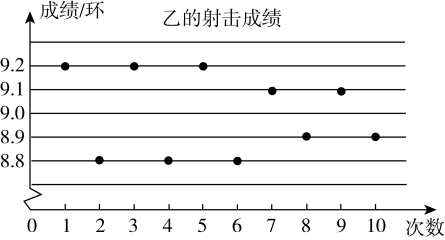

 A、甲 B、乙 C、丙 D、丁7. 一个质地均匀的小正方体,六个面分别标有数字“1”、“2”、“3”、“4”、“5”、“6”,掷小正方体后,观察朝上一面的数字出现偶数的概率是( )A、 B、 C、 D、8. 小华把如图所示的4×4的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等) ,则飞镖落在阴影区域的概率是( )
A、甲 B、乙 C、丙 D、丁7. 一个质地均匀的小正方体,六个面分别标有数字“1”、“2”、“3”、“4”、“5”、“6”,掷小正方体后,观察朝上一面的数字出现偶数的概率是( )A、 B、 C、 D、8. 小华把如图所示的4×4的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等) ,则飞镖落在阴影区域的概率是( ) A、 B、 C、 D、9. 对于两个不相等的实数 ,我们规定符号 表示 中较大的数,如 ,按这个规定,方程 的解为 ( )A、 B、 C、 D、 或-110. 如图,⊙O上有一个动点A和一个定点B,令线段AB的中点是点P,过点B作⊙O的切线BQ,且BQ=3,现测得 的长度是 , 的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )
A、 B、 C、 D、9. 对于两个不相等的实数 ,我们规定符号 表示 中较大的数,如 ,按这个规定,方程 的解为 ( )A、 B、 C、 D、 或-110. 如图,⊙O上有一个动点A和一个定点B,令线段AB的中点是点P,过点B作⊙O的切线BQ,且BQ=3,现测得 的长度是 , 的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )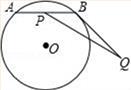 A、3 B、2 C、9 D、10
A、3 B、2 C、9 D、10二、填空题
-
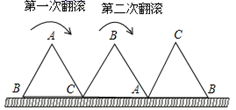
11. 已知 ,n是方程 的两个根,则代数式 的值为 .12. 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,现在从第一个位置翻滚到第三个位置,则B点所经过的路径长度为.
 13. 如图,已知经过原点的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB度数为.
13. 如图,已知经过原点的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB度数为.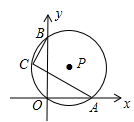 14. 在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为.15. 现有张正面分别标有数字0,1,2,3,4,5的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为 ,则使得关于 的一元二次方程 有实数根,且关于 的分式方程 有解的概率为 .16. 如图,△ABC内接于⊙O , AB是⊙O直径,∠ACB的平分线交⊙O于D , 若AC=m , BC=n , 则CD的长为(用含m、n的代数式表示).
14. 在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为.15. 现有张正面分别标有数字0,1,2,3,4,5的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为 ,则使得关于 的一元二次方程 有实数根,且关于 的分式方程 有解的概率为 .16. 如图,△ABC内接于⊙O , AB是⊙O直径,∠ACB的平分线交⊙O于D , 若AC=m , BC=n , 则CD的长为(用含m、n的代数式表示).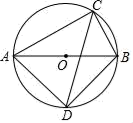
三、解答题
-
17. 解方程:(1)、x2﹣2x﹣1=0;(2)、3(x+2)2=x2﹣4.18. 某商场购进了一批单价为100元的名牌衬衫,当销售价为150元时,平均每天可售出20件,为了扩大销售、增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果衬衫单价每降价1元,商场平均每天可多售出4件,另外,这批衬衫平均每天要扣除其它成本50元,若商场平均每天盈利2 750元,衬衫单价应定为多少元?19. 如图所示,圆O为△ABC的外接圆,AM,AT分别为中线和角平分线,过点B和点C的圆O的切线相交于点P,连结AP,与BC和圆O分别相交于点D、E.

求证:点T是△AME的内心。
20. 请阅读下列材料:问题:已知方程x²+x-1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍。
解:设所求方程的根为y,则y=2x,所以x= 。
把x= 代入已知方程,得( )2+ -1=0
化简,得y2+2y-4=0
故所求方程为y2+2y-4=0。
这种利用方程根的代换求新方程的方法,我们称为“换根法”。
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式)。
(1)、已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为:。(2)、已知关于x的一元二次方程ax2+bx+c=0有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;(3)、已知关于x的方程x2-mx+n=0有两个实数根,求一个方程,使它的根分别是已知方程根的平方。21. 某县教育局为了对该区八年级数学学科教学质量进行检查,对该区八年级的学生进行摸底,为了解摸底的情况,进行了抽样调查,过程如下,请将有关问题补充完整.收集数据:随机抽取 学校与 学校的各20名学生的数学成绩(单位:分)进行分析:
学校
91
89
77
86
71
31
97
93
72
91
81
92
85
85
95
88
88
90
44
91
学校
84
93
66
69
76
87
77
82
85
88
90
88
67
88
91
96
68
97
59
88
(1)、整理、描述数据:按如下数据段整理、描述这两组数据分段
学校
30≤x≤39
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
学校
1
1
0
0
3
7
8
学校
(2)、分析数据:两组数据的平均数、中位数、众数、方差如下表:统计量
学校
平均数
中位数
众数
方差
学校
81.85
88
91
268.43
学校
81.95
86
m
115.25
(3)、得出结论::若 学校有800名八年级学生,估计这次考试成绩80分以上(包含80分)人数为多少人?
:根据表格中的数据,推断出哪所学校学生的数学水平较高,并说明理由.(至少从两个不同的角度说明推断的合理性)
22. 某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题: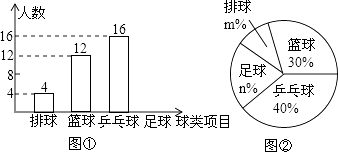 (1)、九(1)班的学生人数为__ , 并把条形统计图补充完整;
(1)、九(1)班的学生人数为__ , 并把条形统计图补充完整;
(2)、扇形统计图中m=10 , n=20 , 表示“足球”的扇形的圆心角是多少度;(3)、排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.23. 如图,10-1、10-2、10-3、…、10-n分别是⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,、…、正n边形ABCD…,点M、N分别从点B,C开始以相同的速度在⊙O上逆时针运动 (1)、求图10-1中∠APN的度数;
(1)、求图10-1中∠APN的度数;
(2)、图10-2中,∠APN的度数是 , 图10-3中∠BPN的度数是。
(3)、试探索∠APN的度数与正多边形边数n的关系(直接写答案)
24. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答:
 (1)、矩形“奇妙四边形”(填“是”或“不是”);(2)、如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.“奇妙四边形”ABCD的面积为;(3)、如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
(1)、矩形“奇妙四边形”(填“是”或“不是”);(2)、如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.“奇妙四边形”ABCD的面积为;(3)、如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.