初中数学苏科版九年级上学期期末复习专题9 数据的离散程度

试卷更新日期：2020-12-09 类型：复习试卷

进入出卷网下载

一、单选题

1. 方差是刻画数据波动程度的量，对于一组数据x1，x2，x3，xn，可用如下算式计算方差： $s^{2} = \frac{1}{n} [{(x_{1} - 5)}^{2} + {(x_{2} - 5)}^{2} + {(x_{3} - 5)}^{2} + ...... + {(x_{n} - 5)}^{2}]$ ，其中“5”是这组数据的（）

A、最小值 B、平均数 C、中位数 D、众数

查看试题解析
2. 甲、乙、丙、丁四位同学五次数学测验的成绩的平均数相同，五次测验的方差如下表．

甲

乙

丙

丁

方差

4

2

55

19

如果从四位同学中选出一位状态稳定的同学参加全国数学联赛，那么应选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
3. 八年级某学生在一次户外活动中进行射击比赛，七次射击成绩依次为（单位：环）：4，5，6，6，6，7，8．则下列说法错误的是（）

A、该组成绩的众数是6环 B、该组成绩的中位数数是6环 C、该组成绩的平均数是6环 D、该组成绩数据的方差是10

查看试题解析
4. 下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位：cm）的平均数和方差．要从中选择一名成绩较高且发挥稳定的运动员参加决赛，最合适的运动员是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 在发生某公共卫生事件期间，有专业机构认为该事件在一段时间没有发生大规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”．根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是（）

A、甲地：总体平均值为3，中位数为4 B、乙地：总体平均值为2，总体方差为3 C、丙地：中位数为2，众数为3 D、丁地：总体平均值为1，总体方差大于0

查看试题解析
6. 下表记录了甲、乙、丙、丁四位跳远运动员选拔赛成绩的平均数与方差：

根据表中信息，请你选择一名成绩好且发挥稳定的选手参赛，最合适的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 小华进行了5次射击训练后，计算出这5次射击的平均成绩为8环，方差为s₁² ，随后小华又进行了第6次射击，成绩恰好是8环，并计算出这6次射击成绩的方差为s₂² ，则下列说法正确的是（）

A、s₁²=s₂² B、s₁²＜s₂² C、s₁²＞s₂² D、无法确定s₁²与s₂²的大小

查看试题解析
8. 若一组数据 $a_{1}$ ， $a_{2}$ ， $a_{3}$ 的平均数为4，方差为3，那么数据 $a_{1} + 2$ ， $a_{2} + 2$ ， $a_{3} + 2$ 的平均数和方差分别是（）

A、4， 3 B、6 $，$ 3 C、3 $，$ 4 D、6 5

查看试题解析
9. 已知一组数据的方差为 $\frac{34}{5}$ ，数据为：－1，0，3，5，x，那么x等于（）

A、－2或5.5 B、2或－5.5 C、4或11 D、－4或－11

查看试题解析
10. 为了解当地气温变化情况，某研究小组记录了寒假期间连续6天的最高气温，结果如下（单位：℃）：﹣6，﹣3，x，2，﹣1，3．若这组数据的中位数是﹣1，则下列结论错误的是（　　）

A、方差是8 B、极差是9 C、众数是﹣1 D、平均数是﹣1

查看试题解析

二、填空题

11. 设甲组数据：6，6，6，6，的方差为 $s_{甲}^{2}$ ，乙组数据：1，1，2的方差为 $s_{乙}^{2}$ ，则 $s_{甲}^{2}$ 与 $s_{乙}^{2}$ 的大小关系是．

查看试题解析
12. 已知一组数据x₁ ， x₂ ， …x_n的方差是2，则另一组数据x₁﹣a，x₂﹣a，…，x_n﹣a的方差是.

查看试题解析

13. 某校为了选拔一名百米赛跑运动员参加市中学生运动会，组织了

6

次预选赛，其中甲，乙两名运动员较为突出，他们在

6

次预选赛中的成绩（单位：秒）如下表所示：

甲	$12.0$	$12.0$	$12.2$	$11.8$	$12.1$	$11.9$
乙	$12.3$	$12.1$	$11.8$	$12.0$	$11.7$	$12.1$

由于甲，乙两名运动员的成绩的平均数相同，学校决定依据他们成绩的稳定性进行选拔，那么被选中的运动员是．

查看试题解析

14. 从甲、乙两种玉米种子中选择一种合适的推荐给某地．考虑到庄稼人对玉米的产量和产量的稳定性十分的关心，选择之前，为了解甲、乙两种玉米种子的情况，某单位各用了10块自然条件相同的试验田进行试验，得到各试验田每公顷产量（单位：t）的数据，这两组数据的平均数分别是 $\bar{x}$ _甲 $\approx 7.5$ ， $\bar{x}$ _乙 $\approx 7.5$ ，方差分别是 $S$ 2甲 $\approx 0.010, S$ 2乙 $\approx 0.002$ ，你认为应该选择的玉米种子是．

查看试题解析
15. 在一次立定跳远测试中，10名学生所测的成绩（单位：厘米）如下：182，160，169，178，180，158，156，163，161，150，则这一组数据中最大值与最小值的差是．

查看试题解析
16. 已知数据 $x_{1}$ ， $x_{2}$ ， $\dots$ ， $x_{n}$ 的平均数为m，方差为 $s^{2}$ ，则数据 $k x_{1} + b$ ， $k x_{2} + b$ ， $\dots$ ， $k x_{n} + b$ 的平均数为，方差为，标准差为.

查看试题解析
17. 已知数据 $x_{1}$ ， $x_{2}$ ， $\dots$ ， $x_{n}$ 的方差是 $0.1$ ，则 $4 x_{1} - 2$ ， $4 x_{2} - 2$ ， $\dots$ ， $4 x_{n} - 2$ 的方差为.

查看试题解析

三、解答题

18. 甲、乙两名射击运动员各进行10次射击，甲的成绩是7，7，8，9，8，9，10，9，9，9．乙的成绩如图所示（单位：环）

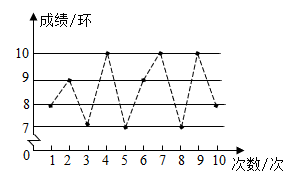(1)、分别计算甲、乙两人射击成绩的平均数；

(2)、若要选拔一人参加比赛，应派哪一位？请说明理由．

查看试题解析
19.
某中学开展“唱红歌”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示．
班级
平均数（分）
中位数
众数
九（1）
85

85
九（2）

80

（1）根据图示填写上表；
（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；
（3）计算两班复赛成绩的方差，并说明哪个班级的成绩较稳定．

查看试题解析
20. 甲、乙两名射击选手各自射击十组，按射击的时间顺序把每组射中靶的环数值记录如下表：

选手
组数 1 2 3 4 5 6 7 8 9 10
甲 98 90 87 98 99 91 91 96 98 96
乙 85 91 89 97 96 97 98 96 98 98
（1）根据上表数据，完成下列分析表：

平均数众数中位数方差[ 极差
甲 94.5
96 15.56 12
乙 94.5

18.65
（2）如果要从甲、乙两名选手中选择一个参加比赛，应选哪一个？为什么？

查看试题解析

四、综合题

21. 在某旅游景区上山的一条小路上，有一些断断续续的台阶．如图是其中的甲、乙段台阶路的示意图．请你用所学过的有关统计知识（平均数、中位数、方差和极差）回答下列问题：

(1)、两段台阶路有哪些相同点和不同点？

(2)、哪段台阶路走起来更舒服，为什么？

(3)、为方便游客行走，需要重新整修上山的小路．对于这两段台阶路，在台阶数不变的情况下，请你提出合理的整修建议．
（图中的数字表示每一级台阶的高度（单位：cm）．并且数据15，16，16，14，14，15的方差S_甲²= $\frac{2}{3}$ ，数据11，15，18，17，10，19的方差S_乙²= $\frac{35}{3}$ ）．

查看试题解析
22. 小云统计了自己所住小区5月1日至30日的厨余垃圾分出量（单位：千克），相关信息如下：
a．小云所住小区5月1日至30日的厨余垃圾分出量统计图：

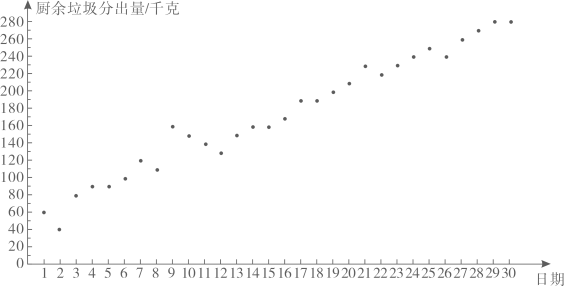
b．小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下：

时段

1日至10日

11日至20日

21日至30日

平均数

100

170

250

(1)、该小区5月1日至30日的厨余垃圾分出量的平均数约为（结果取整数）

(2)、已知该小区4月的厨余垃圾分出量的平均数为60，则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的倍（结果保留小数点后一位）；

(3)、记该小区5月1日至10日的厨余垃圾分出量的方差为 $s_{1}^{2} ，$ 5月11日至20日的厨余垃圾分出量的方差为 $s_{2}^{2}$ ，5月21日至30日的厨余垃圾分出量的方差为 $s_{3}^{2}$ ．直接写出 $s_{1}^{2} ， s_{2}^{2} ， s_{3}^{2}$ 的大小关系．

查看试题解析

23. 2020年3月至5月，某校开展了一系列居家阅读活动．学生利用“宅家”时光，在书海中遨游，从阅读中获得精神慰藉和自我提升．为了解学生居家阅读的情况，学校从七、八两个年级各随机抽取50名学生，进行了居家阅读情况调查．下面给出了部分数据信息：

$a$ ．两个年级学生平均每周阅读时长 $x$ （单位：小时）的频数分布直方图如下（数据分成4组： $0 ⩽ x < 3$ ， $3 \leq x < 6$ ， $6 ⩽ x < 9$ ， $9 ⩽ x ⩽ 12$ ）：

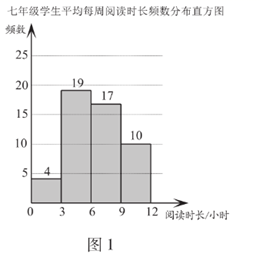
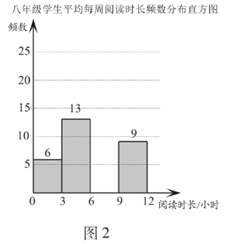
b．七年级学生平均每周阅读时长在 $6 ⩽ x < 9$ 这一组的是：6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8

c．两个年级学生平均每周阅读时长的平均数、中位数、众数、方差如下：

	平均数	中位数	众数	方差
七年级	6.3	m	8	7.0
八年级	6.0	7	7	6.3

根据以上信息，回答下列问题：

(1)、补全图2；

(2)、写出表中m的值；

(3)、返校后，学校计划将平均每周阅读时长不低于9小时的学生授予“阅读之星”称号．小丽说：“根据频数分布直方图中的数据信息，估计七年级约有20%的学生获得该称号，八年级约有18%的学生获得该称号，所以七年级获得该称号的人数一定比八年级获得该称号的人数多．”你认为她的说法（填入“正确”或“不正确”）；

(4)、请你结合数据对两个年级的居家阅读情况进行评价．

查看试题解析

班级	平均数（分）	中位数	众数
九（1）	85		85
九（2）		80

选手组数	1	2	3	4	5	6	7	8	9	10
甲	98	90	87	98	99	91	91	96	98	96
乙	85	91	89	97	96	97	98	96	98	98

时段	1日至10日	11日至20日	21日至30日
平均数	100	170	250

	平均数	众数	中位数	方差[	极差
甲	94.5		96	15.56	12
乙	94.5			18.65