初中数学苏科版九年级上学期期末复习专题6 扇形面积计算
试卷更新日期:2020-12-09 类型:复习试卷
一、单选题
-
1. 一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形圆心角是( )A、120° B、180° C、240° D、300°2. 如图,半径为10的扇形 中, , 为弧AB上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( )
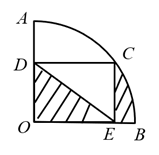 A、 B、 C、 D、3. 如图,在扇形 中,已知 , ,过 的中点C作 , ,垂足分别为D、E,则图中阴影部分的面积为( )
A、 B、 C、 D、3. 如图,在扇形 中,已知 , ,过 的中点C作 , ,垂足分别为D、E,则图中阴影部分的面积为( ) A、 B、 C、 D、4. 如图,AB为半圆O的直径,C为半圆上的一点,OD⊥AC,垂足为D,延长OD与半圆O交于点E.若AB=8,∠CAB=30°,则图中阴影部分的面积为( )
A、 B、 C、 D、4. 如图,AB为半圆O的直径,C为半圆上的一点,OD⊥AC,垂足为D,延长OD与半圆O交于点E.若AB=8,∠CAB=30°,则图中阴影部分的面积为( )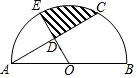 A、 B、 C、 D、5. 如图,等腰直角三角形 中, ,以点C为圆心画弧与斜边 相切于点D,交 于点E,交 于点F,则图中阴影部分的面积是( )
A、 B、 C、 D、5. 如图,等腰直角三角形 中, ,以点C为圆心画弧与斜边 相切于点D,交 于点E,交 于点F,则图中阴影部分的面积是( )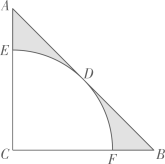 A、 B、 C、 D、6. 如图,将边长为6的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )
A、 B、 C、 D、6. 如图,将边长为6的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )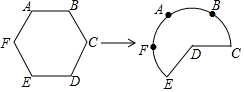 A、S1= S2 B、S1<S2 C、S1=S2 D、S1>S27. 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4 ,则S阴影=( )
A、S1= S2 B、S1<S2 C、S1=S2 D、S1>S27. 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4 ,则S阴影=( )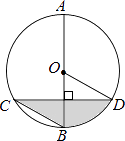 A、2π B、 π C、 π D、 π8. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )
A、2π B、 π C、 π D、 π8. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )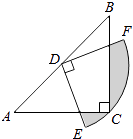 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 一个扇形的面积为 ,半径为6cm,则扇形的圆心角是度.10. 如图,在半径为6的 中,圆心角 ,则阴影部分面积为 .
 11. 如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则以AC和BC的长为两根的一元二次方程是 .
11. 如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则以AC和BC的长为两根的一元二次方程是 .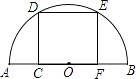 12. 如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为 ,则半圆的半径OA的长为 .
12. 如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为 ,则半圆的半径OA的长为 .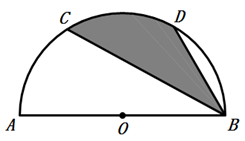 13. 如图,从一块半径为 的圆形铁皮上剪出一个圆周角为120°的扇形 ,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为 .
13. 如图,从一块半径为 的圆形铁皮上剪出一个圆周角为120°的扇形 ,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为 .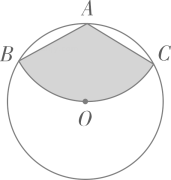 14. 如图,在矩形ABCD中,AB=1,AD= ,P为AD上一个动点,连接BP,线段BA与线段BQ关于BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为.
14. 如图,在矩形ABCD中,AB=1,AD= ,P为AD上一个动点,连接BP,线段BA与线段BQ关于BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为. 15. 如图,在5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与BD交于E,则图中阴影部分的面积为.(结果保留 )
15. 如图,在5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与BD交于E,则图中阴影部分的面积为.(结果保留 ) 16. 如图所示,在Rt△ABC中, , , ,将三角形绕着BC的中点O逆时针旋转 ,点A的对应点为E,则图中阴影部分的面积为.
16. 如图所示,在Rt△ABC中, , , ,将三角形绕着BC的中点O逆时针旋转 ,点A的对应点为E,则图中阴影部分的面积为.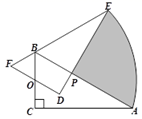
三、解答题
-
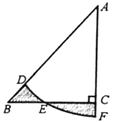
17. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,求AF的长.
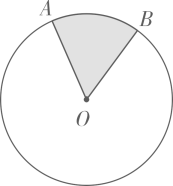
 18. 在附中中心花园的草坪上,有一些自动旋转喷泉水装置,它的喷灌区域是一个扇形,小孙同学想了解这种装置能够喷灌的草坪面积,他测量岀了相关数据,并画出了示意图.如图,这种旋转喷水装置的旋转角度为240°,喷灌起终点A,B两点的距离为12米,求这种装置能够喷灌的草坪面积.
18. 在附中中心花园的草坪上,有一些自动旋转喷泉水装置,它的喷灌区域是一个扇形,小孙同学想了解这种装置能够喷灌的草坪面积,他测量岀了相关数据,并画出了示意图.如图,这种旋转喷水装置的旋转角度为240°,喷灌起终点A,B两点的距离为12米,求这种装置能够喷灌的草坪面积.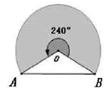 19. 如图,以五边形的每个顶点为圆心,以1为半径画圆,求圆与五边形重合的面积.
19. 如图,以五边形的每个顶点为圆心,以1为半径画圆,求圆与五边形重合的面积.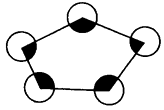
四、综合题
-
20. 如图,已知AB、CD是⊙O的两条平行弦,AB=8,CD=6,弦AB、CD之间的距离为7.
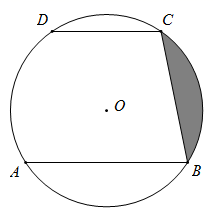 (1)、求证:弧AD=弧BC.(2)、求图中阴影部分的面积.21. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)、求证:弧AD=弧BC.(2)、求图中阴影部分的面积.21. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.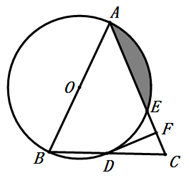 (1)、求证:DF⊥AC;(2)、若⊙O的半径为4,∠C=67.5°,求阴影部分的面积.22. 如图,在平面直角坐标系xOy中,边长为4的正方形ABCD的中心在原点O处,且AB∥x轴,点P在正方形ABCD的边上,点P从点A处沿A→B→C→D→A→B→…匀速运动,以点P为圆心,以1为半径长画圆,在运动过程中:
(1)、求证:DF⊥AC;(2)、若⊙O的半径为4,∠C=67.5°,求阴影部分的面积.22. 如图,在平面直角坐标系xOy中,边长为4的正方形ABCD的中心在原点O处,且AB∥x轴,点P在正方形ABCD的边上,点P从点A处沿A→B→C→D→A→B→…匀速运动,以点P为圆心,以1为半径长画圆,在运动过程中: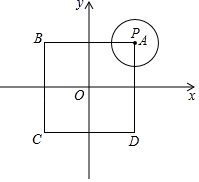 (1)、当⊙P第1次与x轴相切时,则圆心P的坐标为;(直接写出结果)(2)、当圆心P的运动路程为2019时,判断⊙P与y轴的位置关系,并说明理由;(3)、当⊙P第一次回到出发的位置时,即⊙P运动一周,求⊙P运动一周覆盖平面的区域的面积.
(1)、当⊙P第1次与x轴相切时,则圆心P的坐标为;(直接写出结果)(2)、当圆心P的运动路程为2019时,判断⊙P与y轴的位置关系,并说明理由;(3)、当⊙P第一次回到出发的位置时,即⊙P运动一周,求⊙P运动一周覆盖平面的区域的面积.