初中数学苏科版九年级上学期期末复习专题3 圆
试卷更新日期:2020-12-09 类型:复习试卷
一、单选题
-
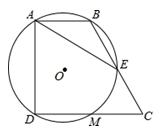
1. 下列说法错误的是( )A、直径是圆中最长的弦 B、长度相等的两条弧是等弧 C、面积相等的两个圆是等圆 D、半径相等的两个半圆是等弧2. 已知MN是⊙O的一条非直径的弦,则下列说法中错误的是( )A、M、N两点到圆心O的距离相等 B、MN是圆的一条对称轴 C、在圆中可画无数条与MN相等的弦 D、圆上有两条弧,一条是优弧,一条是劣弧3. 如图,把一个量角器与一块30°(∠CAB=30° )角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有点P恰好是量角器的半圆弧中点,连结CP。若BC=2,则CP的长为( )
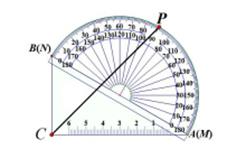 A、 B、 C、 D、4. 楠溪江优美的风光吸引全国各地的旅客前来观赏.如图是景区的一座圆弧形三孔桥,测得最大桥拱的水面宽AB为6m,桥顶C到水面AB的距离CD长为2m,则这座桥桥拱半径为( )
A、 B、 C、 D、4. 楠溪江优美的风光吸引全国各地的旅客前来观赏.如图是景区的一座圆弧形三孔桥,测得最大桥拱的水面宽AB为6m,桥顶C到水面AB的距离CD长为2m,则这座桥桥拱半径为( )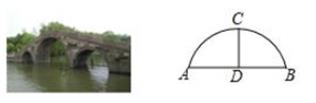 A、3m B、 m C、 m D、5m5. 已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(-3,5) C、(1,2) D、(1,-2)6. 在平面直角坐标系中, 已知点P的坐标为(6,8),若以点P为圆心,12为半径作圆,则坐标原点O与⊙P的位置关系是( )A、点O在⊙P内 B、点O 在⊙P上 C、点O在⊙P外 D、无法确定7. 在△ 中,已知 , , 是 的中点,以 为圆心作一个 为半径的圆 ,则 , , 三点在圆 内的有( )个.
A、3m B、 m C、 m D、5m5. 已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(-3,5) C、(1,2) D、(1,-2)6. 在平面直角坐标系中, 已知点P的坐标为(6,8),若以点P为圆心,12为半径作圆,则坐标原点O与⊙P的位置关系是( )A、点O在⊙P内 B、点O 在⊙P上 C、点O在⊙P外 D、无法确定7. 在△ 中,已知 , , 是 的中点,以 为圆心作一个 为半径的圆 ,则 , , 三点在圆 内的有( )个.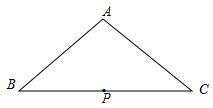 A、0 B、1 C、2 D、38. 如图,▱ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A、0 B、1 C、2 D、38. 如图,▱ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )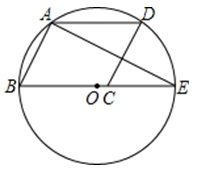 A、36° B、46° C、27° D、63°9. 如图,是小飞同学的答卷,他的得分应该是( )
A、36° B、46° C、27° D、63°9. 如图,是小飞同学的答卷,他的得分应该是( ) A、40分 B、60分 C、80分 D、100分10. 线段AB上有一动点C(不与A,B重合),分别以AC,BC为边向上作等边△ACM和等边△BCN,点D是MN的中点,连结AD,BD,在点C的运动过程中,有下列结论:①△ABD可能为直角三角形;②△ABD可能为等腰三角形;③△CMN可能为等边三角形;④若AB=6,则AD+BD的最小值为
A、40分 B、60分 C、80分 D、100分10. 线段AB上有一动点C(不与A,B重合),分别以AC,BC为边向上作等边△ACM和等边△BCN,点D是MN的中点,连结AD,BD,在点C的运动过程中,有下列结论:①△ABD可能为直角三角形;②△ABD可能为等腰三角形;③△CMN可能为等边三角形;④若AB=6,则AD+BD的最小值为 . 其中正确的是( )
. 其中正确的是( )  A、②③ B、①②③④ C、①③④ D、②③④
A、②③ B、①②③④ C、①③④ D、②③④二、填空题
-
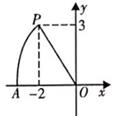
11. 如图,点 ,以点O为圆心,以 的长为半径画弧,交x轴的负半轴于点A,则点A的坐标为.
 12. 如图,P是⊙O的直径BA延长线上一点,PD交⊙O于点C,且PC=OD,如果∠P=24°,则∠DOB=.
12. 如图,P是⊙O的直径BA延长线上一点,PD交⊙O于点C,且PC=OD,如果∠P=24°,则∠DOB=.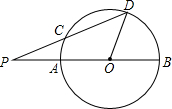 13. 如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若 的度数为35°,则 的度数是.
13. 如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若 的度数为35°,则 的度数是.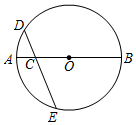 14. 我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点 到以原点为圆心,以1为半径的圆的距离为 .
14. 我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点 到以原点为圆心,以1为半径的圆的距离为 . 15. 半径分别为3cm与 cm的⊙O1与⊙O2相交于A、B两点,如果公共弦AB= cm,那么圆心距O1O2的长为cm.16. 如图,点P在以MN为直径的半圆上运动,(点P与M,N不重合) 平分 ,交PM于点E,交PQ于点F.
15. 半径分别为3cm与 cm的⊙O1与⊙O2相交于A、B两点,如果公共弦AB= cm,那么圆心距O1O2的长为cm.16. 如图,点P在以MN为直径的半圆上运动,(点P与M,N不重合) 平分 ,交PM于点E,交PQ于点F.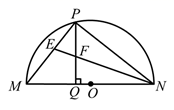 (1)、 .(2)、若 ,则 .17. 如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:
(1)、 .(2)、若 ,则 .17. 如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:①DM=CM;②弧AB=弧EM;③⊙O的直径为2;④AE=AD.
其中正确的结论有(填序号).
 18. 如图,AB是⊙O的直径,AB=4 ,C为弧AB中点,点P是⊙O上一个动点,取弦AP的中点D,则CD的最大值为.
18. 如图,AB是⊙O的直径,AB=4 ,C为弧AB中点,点P是⊙O上一个动点,取弦AP的中点D,则CD的最大值为.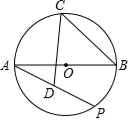
三、解答题
-
19. 2020年8月,今年第4号台风“黑格比”来袭,宁波市某镇被雨水“围攻”,如图,当地有一拱桥为圆弧形,跨度AB=24米,拱高PM=8米,当洪水泛滥,水面跨度缩小到8米时要采取紧急措施,当时测量人员测得水面A1B1到拱顶距离只有1米,问是否需要采取紧急措施?请说明理由.
 20. 把球放在长方体纸盒内,球的一部分露出盒外,如下所示为正视图.已知EF=CD=16厘米,求出这个球的半径.
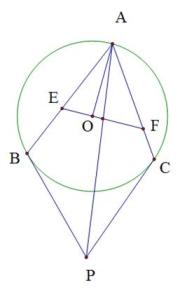
20. 把球放在长方体纸盒内,球的一部分露出盒外,如下所示为正视图.已知EF=CD=16厘米,求出这个球的半径.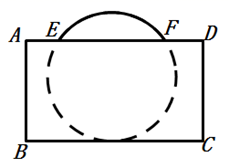 21. 如图,锐角三角形ABC内接于圆O,过圆心O且垂直于半径OA的直线分别交AB、AC于点E、F. 设圆O在B、C两点处的切线交于点P.
21. 如图,锐角三角形ABC内接于圆O,过圆心O且垂直于半径OA的直线分别交AB、AC于点E、F. 设圆O在B、C两点处的切线交于点P.证明:直线AP平分线段EF.
 22. 如图,AB为⊙O直径,C为⊙O上一点,点D是 的中点,DE⊥AC于E,DF⊥AB于F.
22. 如图,AB为⊙O直径,C为⊙O上一点,点D是 的中点,DE⊥AC于E,DF⊥AB于F.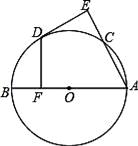 (1)、判断DE与⊙O的位置关系,并证明你的结论;(2)、若OF=4,求AC的长度.
(1)、判断DE与⊙O的位置关系,并证明你的结论;(2)、若OF=4,求AC的长度.四、综合题
-
23. 如图,AB是⊙O的直径,C是 的中点,CE⊥AB于点E,BD交CE于点F。
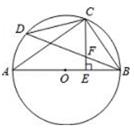 (1)、求证: CF=BF;(2)、若CD=6,AC=8,求⊙O的半径及CE的长。24. 已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=40°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)、求证: CF=BF;(2)、若CD=6,AC=8,求⊙O的半径及CE的长。24. 已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=40°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.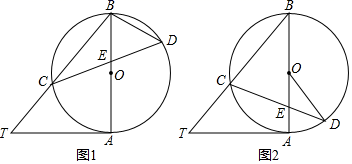 (1)、如图1,求∠T和∠CDB的度数;(2)、如图2,当BE=BC时,求∠CDO的度数.25. 如图,A、B是⊙O上的两个点,已知P为平面内一点,(P、A、B三点不在同一条直线上).
(1)、如图1,求∠T和∠CDB的度数;(2)、如图2,当BE=BC时,求∠CDO的度数.25. 如图,A、B是⊙O上的两个点,已知P为平面内一点,(P、A、B三点不在同一条直线上).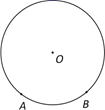 (1)、若点P在⊙O上,⊙O的半径为1.
(1)、若点P在⊙O上,⊙O的半径为1.①当∠APB=45°时,AB的长度为;
②当AB=1时,∠APB= °;
(2)、若点P不在⊙O上,直线PA、PB交⊙O于点C、D(点C与点A、点D与点B均不重合),连接AD,设∠CAD= ,∠ADB= ,试用 、 表示∠APB(请直接写出答案,并画出示意图).