初中数学苏科版2020-2021学年八年级上学期期末模拟试卷
试卷更新日期:2020-12-09 类型:期末考试
一、单选题
-
1. 下列四种垃圾分类回收标识中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 的算术平方根是( )A、4 B、±2 C、2 D、3. 已知点(1-2a , a-4)在第三象限,则整数a的值可以取( )个.
2. 的算术平方根是( )A、4 B、±2 C、2 D、3. 已知点(1-2a , a-4)在第三象限,则整数a的值可以取( )个.
A、1 B、2 C、3 D、44. 到三角形三边的距离相等的点是( )A、三角形三内角平分线的交点; B、三角形三边中线的交点; C、三角形三边高的交点; D、三角形三边中垂线的交点。5. 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若∠MON=35°,则∠GOH=( ) A、60° B、70° C、80° D、90°6. 如图, 中, BP平分∠ABC, AP⊥BP于P,连接PC,若 的面积为3.5cm2 , 的面积为4.5cm2 , 则 的面积为( ).
A、60° B、70° C、80° D、90°6. 如图, 中, BP平分∠ABC, AP⊥BP于P,连接PC,若 的面积为3.5cm2 , 的面积为4.5cm2 , 则 的面积为( ).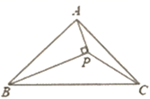 A、0.25cm2 B、0.5 cm2 C、1cm2 D、1.5cm27. 如图, 和 都是等边三角形,点 、 、 在同一条直线上, 、 分别与 、 交于点 、 , 和 交于点 ,有如下结论:① 是等边三角形;② ;③ ≌ ;④ ;⑤ 平分 ;⑥ ;⑦ .其中错误的结论的个数是( )
A、0.25cm2 B、0.5 cm2 C、1cm2 D、1.5cm27. 如图, 和 都是等边三角形,点 、 、 在同一条直线上, 、 分别与 、 交于点 、 , 和 交于点 ,有如下结论:① 是等边三角形;② ;③ ≌ ;④ ;⑤ 平分 ;⑥ ;⑦ .其中错误的结论的个数是( ) A、1 B、2 C、3 D、48. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2 EF,则正方形ABCD的面积为( )
A、1 B、2 C、3 D、48. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2 EF,则正方形ABCD的面积为( ) A、11S B、12S C、13S D、14S9. 如图, 直线 与 轴、 轴分别交于点 和点 ,点 、 分别为线段 、 的中点, 点 为 上一动点, 当 最小时, 点 的坐标为
A、11S B、12S C、13S D、14S9. 如图, 直线 与 轴、 轴分别交于点 和点 ,点 、 分别为线段 、 的中点, 点 为 上一动点, 当 最小时, 点 的坐标为 A、 B、 C、 , D、 ,10. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1.5小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t= 或t= ,其中正确的结论有( )
A、 B、 C、 , D、 ,10. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1.5小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t= 或t= ,其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 已知,函数y=3x+b的图象经过点A(﹣1,y1),点B(﹣2,y2),则y1y2(填“>”“<”或“=”)12. 已知△ABC≌△DEF ,△DEF 的周长为32cm ,DE = 9cm ,EF = 12cm ,则 AC =cm .13. 若点 到 两坐标轴的距离相等,则a的值为14. 一个等腰三角形的底边长为5,一条腰上的中线把周长分成的两部分的差为2,则这个等腰三角形的腰长为.15. △ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为厘米/秒,△BPD与△CQP全等.
 16. 如图,一圆柱体的底面周长为 ,高 为 , 是直径,一只蚂蚁从点 出发沿着圆柱体的表面爬行到点 的最短路程是 .
16. 如图,一圆柱体的底面周长为 ,高 为 , 是直径,一只蚂蚁从点 出发沿着圆柱体的表面爬行到点 的最短路程是 .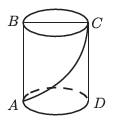 17. 如图,在平面直角坐标系中,点A1 , A2 , A3…都在x轴上,点B1 , B2 , B3…都在直线 上,△OA1B1 , △B1A1A2 , △B2B1A2 , △B2A2A3 , △B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是.
17. 如图,在平面直角坐标系中,点A1 , A2 , A3…都在x轴上,点B1 , B2 , B3…都在直线 上,△OA1B1 , △B1A1A2 , △B2B1A2 , △B2A2A3 , △B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是. 18. 如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积 .
18. 如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积 .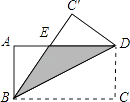 19. 如图,在一张直角三角形纸片ABC中,∠ACB=90°,∠A=30°P是边AB上的一动点,将△ACP沿着CP折叠至△A1CP , 当△A1CP与△ABC的重叠部分为等腰三角形时,则∠ACP的度数为 .
19. 如图,在一张直角三角形纸片ABC中,∠ACB=90°,∠A=30°P是边AB上的一动点,将△ACP沿着CP折叠至△A1CP , 当△A1CP与△ABC的重叠部分为等腰三角形时,则∠ACP的度数为 .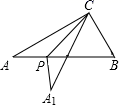 20. 如图,AD是△ABC的角分平线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一动点,当△BDF为直角三角形时,则∠ADF的度数为.
20. 如图,AD是△ABC的角分平线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一动点,当△BDF为直角三角形时,则∠ADF的度数为.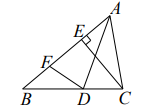
三、解答题
-
21. 解方程(1)、 .(2)、 .22. 如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
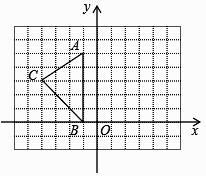 (1)、求出△ABC的面积.(2)、在图中作出△ABC关于y轴的对称图形△A1B1C1 .(3)、写出点△A1B1C1的坐标.23. 已知:如图,在△AOB和△COD中,OA=OB,OC=OD.,若∠AOB=∠COD=60°,
(1)、求出△ABC的面积.(2)、在图中作出△ABC关于y轴的对称图形△A1B1C1 .(3)、写出点△A1B1C1的坐标.23. 已知:如图,在△AOB和△COD中,OA=OB,OC=OD.,若∠AOB=∠COD=60°,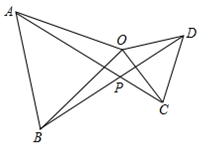
①求证:AC=BD;
②求∠APB的度数.
24. 台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向 由 行驶向 ,已知点 为一海港,且点 与直线 上的两点 , 的距离分别为 , ,又 ,以台风中心为圆心周围 以内为受影响区域. (1)、求 的度数.(2)、海港 受台风影响吗?为什么?(3)、若台风的速度为20千米/小时,当台风运动到点 处时,海港 刚好受到影响,当台风运动到点 时,海港 刚好不受影响,即 ,则台风影响该海港持续的时间有多长?25. 在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别作出了一次函数 和 的图象,分别与x轴交于点A、B,两直线交于点C. 已知点 , ,观察图象并回答下列问题:
(1)、求 的度数.(2)、海港 受台风影响吗?为什么?(3)、若台风的速度为20千米/小时,当台风运动到点 处时,海港 刚好受到影响,当台风运动到点 时,海港 刚好不受影响,即 ,则台风影响该海港持续的时间有多长?25. 在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别作出了一次函数 和 的图象,分别与x轴交于点A、B,两直线交于点C. 已知点 , ,观察图象并回答下列问题: (1)、关于x的方程 的解是;关于x的不等式 的解集是;(2)、直接写出关于x的不等式组 的解集;(3)、若点 ,求关于x的不等式 的解集和△ABC的面积.26. 随着生活水平的逐步提高,某单位的私家小轿车越来越多,为确保有序停车,单位决定筹集资金维修和新建一批停车棚.该单位共有42辆小轿车,准备维修和新建的停车棚共有6个,费用和可供停车的辆数及用地情况如下表:
(1)、关于x的方程 的解是;关于x的不等式 的解集是;(2)、直接写出关于x的不等式组 的解集;(3)、若点 ,求关于x的不等式 的解集和△ABC的面积.26. 随着生活水平的逐步提高,某单位的私家小轿车越来越多,为确保有序停车,单位决定筹集资金维修和新建一批停车棚.该单位共有42辆小轿车,准备维修和新建的停车棚共有6个,费用和可供停车的辆数及用地情况如下表:停车棚
费用(万元/个)
可停车的辆数(辆/个)
占地面积(m2/个)
新建
4
8
100
维修
3
6
80
已知可支配使用土地面积为580m2 , 若新建停车棚 个,新建和维修的总费用为 万元.
(1)、求 与 之间的函数关系;(2)、满足要求的方案有几种?(3)、为确保工程顺利完成,单位最少需要出资多少万元.