初中数学苏科版九年级上学期期末复习专题7 圆锥的侧面积

试卷更新日期：2020-12-09 类型：复习试卷

进入出卷网下载

一、单选题

1. 一个圆锥的底面半径是 $4cm$ ，其侧面展开图的圆心角是120°，则圆锥的母线长是（）

A、 $8cm$ B、 $12cm$ C、 $16cm$ D、 $24cm$

查看试题解析
2. 已知圆锥的底面半径为 $2 c m$ ，母线长为 $4 c m$ ，则圆锥的侧面积是（）

A、 $10 c m^{2}$ B、 $10 π c m^{2}$ C、 $8 c m^{2}$ D、 $8 π c m^{2}$

查看试题解析
3. 云南是全国拥有少数民族数量最多的省份，风俗文化多种多样，使得“云南十八怪”成为云南旅游文化的一张名片，图①是十八怪中的“草帽当锅盖”，图②是一个草帽的三视图，根据图中所给的数据计算出该草帽的侧面积为（）

A、 $240 π c m^{2}$ B、 $576 π c m^{2}$ C、 $624 π c m^{2}$ D、 $120 π c m^{2}$

查看试题解析
4. 一个圆锥的主视图是边长为6cm的正三角形，则这个圆锥的侧面积等于（　　）

A、36 πcm² B、24πcm² C、18πcm² D、12 πcm²

查看试题解析
5. 用一圆心角为120°，半径为6cm的扇形做成一个圆锥的侧面，则这个圆锥的底面半径是（）

A、1cm B、2cm C、3cm D、6cm

查看试题解析
6. 如图，正方形 $A B C D$ 的边长为4，以点A为圆心， $A D$ 为半径画圆弧 $D E$ 得到扇形 $D A E$ （阴影部分，点E在对角线 $A C$ 上）.若扇形 $D A E$ 正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是（）

A、 $\sqrt{2}$ B、1 C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
7. 用一个半径为 $3 ，$ 面积为 $3 π$ 的扇形铁皮，制作一个无底的圆锥(不计损耗)，则圆锥的底面半径为（）

A、 $π$ B、 $2 π$ C、2 D、1

查看试题解析
8. 如图，从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形，将剪下的扇形围成一个圆锥，圆锥的高是（）m．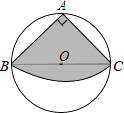

A、4 $\sqrt{2}$ B、5 C、 $\sqrt{30}$ D、2 $\sqrt{15}$

查看试题解析
9. 正如我们小学学过的圆锥体积公式V= $\frac{1}{3}$ πr²h（π表示圆周率，r表示圆锥的底面半径，h表示圆锥的高）一样，许多几何量的计算都要用到π．祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家，创造了当时世界上的最高水平，差不多过了1000年，才有人把π计算得更精确．在辉煌成就的背后，我们来看看祖冲之付出了多少．现在的研究表明，仅仅就计算来讲，他至少要对9位数字反复进行130次以上的各种运算，包括开方在内．即使今天我们用纸笔来算，也绝不是一件轻松的事情，何况那时候没有现在的纸笔，数学计算不是用现在的阿拉伯数字，而是用算筹（小竹棍或小竹片）进行的，这需要怎样的细心和毅力啊！他这种严谨治学的态度，不怕复杂计算的毅力，值得我们学习．
下面我们就来通过计算解决问题：已知圆锥的侧面展开图是个半圆，若该圆锥的体积等于9 $\sqrt{3}$ π，则这个圆锥的高等于（）

A、 $5 \sqrt{3} π$ B、 $5 \sqrt{3}$ C、 $3 \sqrt{3} π$ D、 $3 \sqrt{3}$

查看试题解析

二、填空题

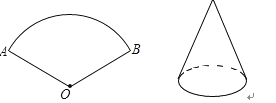
10. 用半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆的半径为．

查看试题解析
11. 圆锥的主视图是一个等边三角形，该圆锥的侧面展开图扇形的圆心角度数为.

查看试题解析
12. 圆锥的底面半径为3，侧面积为 $12 π$ ，则这个圆锥的母线长为.

查看试题解析
13. 用半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.

查看试题解析
14. 一个圆锥的底面半径为3，高为4，则此圆锥的侧面积为.

查看试题解析
15. 两个底面积相等的圆柱和圆锥形杯子，其中圆柱形杯子的 $\frac{1}{2}$ 盛有水，将水倒入圆锥形的杯子中刚好倒满，则圆柱形杯子的高与圆锥形杯子的高的比是。

查看试题解析
16.
如图，将弧长为6π，圆心角为120°的圆形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合（粘连部分忽略不计）则圆锥形纸帽的高是．

查看试题解析

三、解答题

17. 如图，已知圆锥底面⊙O的直径BC=6，高AO=4求该圆锥侧面展开图的面积。

查看试题解析
18. 小明同学用纸板制作了一个圆锥形漏斗模型，如图所示，它的底面半径 $O B = 3 c m$ ，高 $O C = 4 c m$ ，求这个圆锥形漏斗的侧面积．

查看试题解析
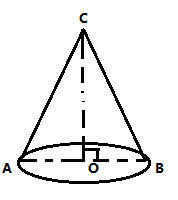19. 如图，圆柱的底面周长为6 $c m$ ， $A C$ 是底面圆的直径，高 $B C = 6 c m$ ， $P$ 是 $B C$ 上一点且 $P C = \frac{2}{3} B C$ .一只蚂蚁从点 $A$ 出发沿着圆柱的侧面爬行到点 $P$ ，求爬行的最短路程是多少.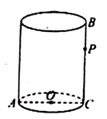

查看试题解析

四、作图题

20. 一个等腰Rt△ABC如图所示，将它绕着直线AC旋转一周，形成一个几何体.

(1)、画出这个几何体的三视图.

(2)、依据图中的测量数据，计算这个几何体的表面积.

查看试题解析

五、综合题

21. 如图，一个圆锥的高为 $3 \sqrt{3}$ cm，侧面展开图是半圆．求：

(1)、圆锥的母线长与底面半径之比；

(2)、求∠BAC的度数；

(3)、圆锥的侧面积（结果保留π）．

查看试题解析