初中数学苏科版九年级上学期期末复习专题4 正多边形与圆
试卷更新日期:2020-12-09 类型:复习试卷
一、单选题
-
1. 圆内接正六边形的边长为3,则该圆的直径长为( )A、3 B、3 C、3 D、62. 如图,若干全等正五边形排成环状.图中所示的是前3个正五边形,则要完成这一圆环还需( )个这样的正五边形
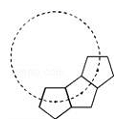 A、6 B、7 C、8 D、93. 如图A,B,C是 上顺次3点,若 , , 分别是 内接正三角形、正方形、正n边形的一边,则 ( )
A、6 B、7 C、8 D、93. 如图A,B,C是 上顺次3点,若 , , 分别是 内接正三角形、正方形、正n边形的一边,则 ( ) A、9 B、10 C、12 D、154. 如图,以正五边形 的对角线 为边,作正方形 使点 落在正方形 内,则 的度数为( )
A、9 B、10 C、12 D、154. 如图,以正五边形 的对角线 为边,作正方形 使点 落在正方形 内,则 的度数为( )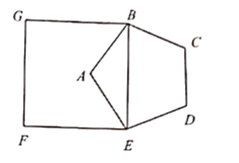 A、 B、 C、 D、5. 在圆内接正方形ABCD中,正方形的边长AB是8,则这个正方形的中心角和边心距是( )A、90°,4 B、90°,1 C、45°,4 D、45°,16.
A、 B、 C、 D、5. 在圆内接正方形ABCD中,正方形的边长AB是8,则这个正方形的中心角和边心距是( )A、90°,4 B、90°,1 C、45°,4 D、45°,16.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
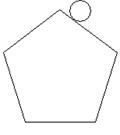 A、4 B、5 C、6 D、107. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A、4 B、5 C、6 D、107. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )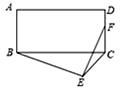 A、 B、4 C、5 D、8. 我国古代伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1)。刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法。如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结AG,CF,AG交CF于点P,若AP=2 ,则 的长为( )
A、 B、4 C、5 D、8. 我国古代伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1)。刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法。如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结AG,CF,AG交CF于点P,若AP=2 ,则 的长为( )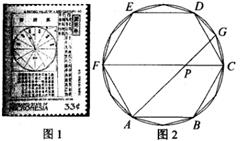 A、 B、 π C、 π D、 π
A、 B、 π C、 π D、 π二、填空题
-
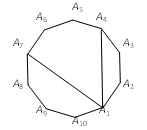
9. 边长为2的正六边形的边心距为。10. 正六边形的外接圆的半径与内切圆的半径之比为.11. 已知正六边形的外接圆的半径是 ,则正六边形的周长是 .12. 如图,在正十边形A1A2A3A4A5A6A7A8A9A10中,连接A1A4、A1A7 , 则∠A4A1A7=°.
 13. 如图,在边长为 的正六边形 中,点P在BC上,则 的面积为.
13. 如图,在边长为 的正六边形 中,点P在BC上,则 的面积为.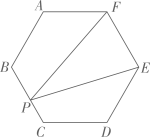 14. 刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径 .此时圆内接正六边形的周长为 ,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为.(参考数据: )
14. 刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径 .此时圆内接正六边形的周长为 ,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为.(参考数据: )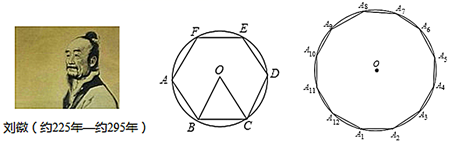 15. 如图,正方形 和正 都内接于半径为1的 , 与 、 分别相交于点 、 ,则 的长为.
15. 如图,正方形 和正 都内接于半径为1的 , 与 、 分别相交于点 、 ,则 的长为.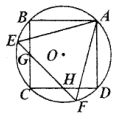 16. 如图,作半径为2的⊙O的内接正四边形ABCD,然后作正四边形ABCD的内切圆,得第二个圆,再作第二个圆的内接正四边形A1B1C1D1 , 又作正四边形A1B1C1D1的内切圆,得第三个圆…,如此下去,则第六个圆的半径为 .
16. 如图,作半径为2的⊙O的内接正四边形ABCD,然后作正四边形ABCD的内切圆,得第二个圆,再作第二个圆的内接正四边形A1B1C1D1 , 又作正四边形A1B1C1D1的内切圆,得第三个圆…,如此下去,则第六个圆的半径为 .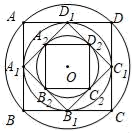
三、解答题
-
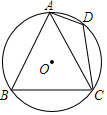
17. 如图,已知正三角形ABC内接于 ,AD是 的内接正十二边形的一条边长,连接CD,若 ,求 的半径.
 18. 如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
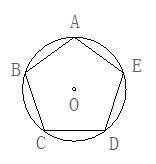
18. 如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积. 19. 如图五边形ABCDE内接于⊙O,∠A =∠B=∠C=∠D=∠E.
19. 如图五边形ABCDE内接于⊙O,∠A =∠B=∠C=∠D=∠E.求证:五边形ABCDE是正五边形
四、作图题
-
20. 尺规作图:如图,AD为⊙O的直径。
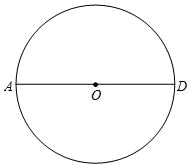 (1)、求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);(2)、已知连接DF,⊙O的半径为4,求DF的长。
(1)、求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);(2)、已知连接DF,⊙O的半径为4,求DF的长。五、综合题
-
21. 如图,正五边形ABCD中,点F、G分别是BC、CD的中点,AF与BG相交于H.
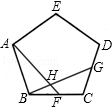 (1)、求证:△ABF≌△BCG;(2)、求∠AHG的度数.22. 已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.
(1)、求证:△ABF≌△BCG;(2)、求∠AHG的度数.22. 已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.
现商家设计了2种棱柱体包装盒,其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率= ×100%)
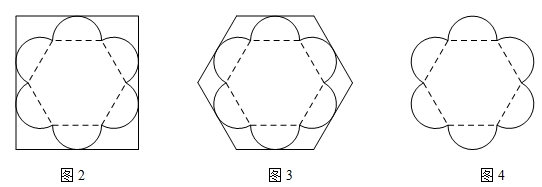 (1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%);(2)、考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.
(1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%);(2)、考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.
-