浙江省衢州市2021届九年级上学期数学期中考试试卷

试卷更新日期：2020-12-09 类型：期中考试

进入 出卷网 下载

一、选择题（本题共有10小题，每小题3分，共30分）

  • 1. 在下列函数表达式中，一定为二次函数的是（   ）
    A、y=x+3 B、y=ax2+bx+c C、y=t2－2t+2 D、y=x2+ 1x

    查看试题解析

  • 2. 对“某市明天下雨的概率是85%”这句话，理解正确的是（   ）
    A、某市明天将有85%的时间下雨 B、某市明天将有85%的地区下雨 C、某市明天一定下雨 D、某市明天下雨的可能性较大

    查看试题解析

  • 3. 如图，点A，B，C，D在⊙O上，BC是⊙O的直径．若∠D=36°，则∠BCA等于（   ）

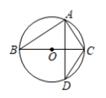    A、72° B、54° C、45° D、36°

    查看试题解析

  • 4. 将二次函数y=x2－4x+3化为y=a(x－m)2+k的形式，下列结果正确的是（   ）
    A、y=(x－2)2－1 B、y=(x－2)2+1 C、y=(x+2)2－1 D、y=(x+2)2+1

    查看试题解析

  • 5. 某小组在做“用频率估计概率”的试验时，绘出的某一结果出现的频率折线图如图所示，则符合这一结果的试验可能是（   ）

    A、抛一枚硬币，出现正面朝上 B、掷一个正六面体的骰子，出现3点朝上 C、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃 D、从一个装有2个红球、1个黑球的袋子中任取一球，取到的是黑球

    查看试题解析

  • 6. 若刻度尺与⊙O按如图位置摆放，有刻度的一边与⊙O的两个交点处的读数如图所示（单位：cm），⊙O的半径是5cm，则圆心O到刻度尺的距离为（   ）

    A、5cm B、4cm C、3cm D、2cm

    查看试题解析

  • 7. 如图，已知AB是⊙O的直径，弦CD⊥AB于点E，G是 AB⌢ 的中点，连结AD，AG，GD，则下列结论不一定成立的是（   ）

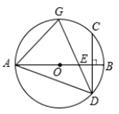    A、CE=DE B、∠GDC=∠BAD C、∠AGD=∠ADC D、∠ADG=∠GAB

    查看试题解析

  • 8. 已知A(－3，y1)，B(－2，y2)，C(2，y3)是抛物线y=－(x+1)2+3上的三点，则y1 ， y2 ， y3的大小关系为（   ）
    A、y1<y2<y3 B、y1<y3<y2 C、y3<y2<y1 D、y3<y1<y2

    查看试题解析

  • 9. 如图，将 Δ ABC绕点C顺时针旋转，点B的对应点为点E，点A的对应点为点D，当点E恰好落在AC边上时，连结AD，若∠DAC=75°，AC=2BC=2，则图中阴影部分的面积为（   ）

    A、π4 B、π2 C、π6 D、π3

    查看试题解析

  • 10. 如图，抛物线y=x2－6x+8与x轴交于A，B两点，过点B的直线与抛物线交于点C（点C在x轴上方），过A，B，C三点的⊙M满足∠CAB=45°，则点C的坐标为（   ）

    A、(5，4) B、(4，4) C、(5，3) D、(4，3)

    查看试题解析

二、填空题（本题共有6小题，每小题4分，共24分）

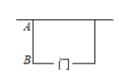
  • 11. 抛物线y=－(x+1)2+3与y轴的交点坐标是 ．

    查看试题解析

  • 12. 一个不透明的袋子中有2个红球和3个黄球，它们除颜色外其余均相同，随机摸出一个小球，摸出红色小球的概率是 ．

    查看试题解析

  • 13. 一个圆的内接四边形ABCD的内角∠A∶∠C=1∶3，则∠C= ．

    查看试题解析

  • 14. 如图，用长为16m的篱笆，一面利用墙（墙足够长）围成一块留有一扇1m宽的门的长方形花圃．设花圃的宽AB为xm，面积为ym2 ， 则y与x的函数表达式为 ．

    查看试题解析

  • 15. 如图，AC是⊙O的直径，弦BD⊥AC于点E，连结BC，过点O作OF⊥BC于点F．若BD=12cm，CE=18cm，则OF的长度为.

    查看试题解析

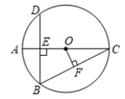  • 16. 如图，抛物线y=x2在第二象限内经过的整点（横坐标、纵坐标都为整数的点）依次为A1 ， A2 ， A3 ， …，An ． 将抛物线y=x2沿直线y=－x向上平移，得到一系列抛物线，这一系列抛物线的顶点M1 ， M2 ， M3 ， …，Mn都在直线y=－x上，同时抛物线依次经过点A1 ， A2 ， A3 ， …，An ， 则顶点M2的坐标是 ， 顶点M2020的坐标是 ．

    查看试题解析

三、解答题（本题共有8小题，第17~19小题每小题6分，第20~21小题每小题8分，第22~23小题每小题10分，第24小题12分，共66分．）

  • 17. 如图，一圆弧过网格的格点A，B，C，网格的单位长度为1．

    (1)、仅用一把无刻度的直尺，利用网格，找出该圆弧的圆心；
    (2)、求弧AC的长．

    查看试题解析

  • 18. 为了解学生的艺术特长发展情况，某校音乐组决定围绕在“舞蹈、乐器、声乐、戏曲、其他活动”项目中，你最喜欢哪一项活动（每人只限一项）的问题，在全校范围内随机抽取部分学生进行问卷调查，并将调查结果绘制成如下两幅不完整的统计图．请你根据统计图解答下列问题：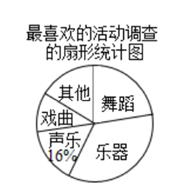

     

    (1)、求这次调查的学生总人数，以及扇形统计图中最喜欢“戏曲”部分扇形的圆心角度数；
    (2)、请你补全条形统计图；
    (3)、若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组，请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率．

    查看试题解析

  • 19. 如图，AB是⊙O的直径，点C，D在⊙O上，已知∠ABD=45°，BC=6，AC=8．

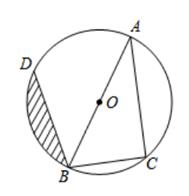    (1)、求BD的长；
    (2)、求图中阴影部分的面积．

    查看试题解析

  • 20. 如图，抛物线y=x2+bx+c与x轴交于A(－1，0)和B(3，0)两点，交y轴于点E．

    (1)、求此抛物线的函数表达式；
    (2)、若直线y=x+1与抛物线交于A，D两点，与y轴交于点F，连接DE，求 Δ DEF的面积．

    查看试题解析

  • 21. 如图，AE是⊙O的直径，点B，C在⊙O上，连结BE，AB，CE，CE是∠AEB的平分线，连结OC交AB于点D．

    (1)、若∠BEC=26°，求∠AOC的度数；
    (2)、若∠CEA=∠A，EC=6，求⊙O的半径．

    查看试题解析

  • 22. 某网店销售一种儿童玩具，进价为每件30元，物价部门规定每件儿童玩具的销售利润不高于进价的50%．在销售过程中发现：当销售单价为35元时，每天可售出350件，若销售单价每提高5元，则每天销售量减少50件．设销售单价为x元（销售单价不低于35元）．
    (1)、当这种儿童玩具以每件最高价出售时，每天的销售量为多少件？
    (2)、求这种儿童玩具每天获得的利润w（元）与销售单价x（元）之间的函数表达式；
    (3)、当销售单价为多少元时，该网店销售这种儿童玩具每天获得的利润最大，最大利润是多少元？

    查看试题解析

  • 23. 如图1，皮皮小朋友燃放一种手持烟花，这种烟花每隔1.6秒发射一发花弹，每一发花弹的飞行路径，爆炸时的高度均相同．皮皮小朋友发射出的第一发花弹的飞行高度h（米）随飞行时间t（秒）变化的规律如下表．

    t/秒

    0

    0.5

    1

    1.5

    2

    2.5

    3

    3.5

    4

    ……

    h/米

    1.8

    7.3

    11.8

    15.3

    17.8

    19.3

    19.8

    19.3

    17.5

    ……

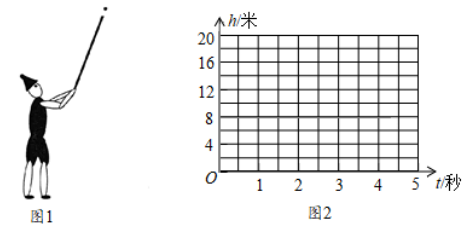    (1)、根据这些数据在图2的直角坐标系中画出相应的点，选择适当的函数表示h（米）与t（秒）之间的关系，并求出相应的函数表达式；
    (2)、当第一发花弹发射2秒后，第二发花弹达到的高度为多少米？
    (3)、为了安全，要求花弹爆炸时的高度不低于18米．皮皮发现在第一发花弹爆炸的同时，第二发花弹与它处于同一高度，请分析花弹的爆炸高度是否符合安全要求

    查看试题解析

  • 24. 如图

    (1)、知识储备

    ①如图1，已知点P为等边三角形ABC外接圆的 BC⌢ 上任意一点．求证：PB+PC=PA；

    ②定义：在 Δ ABC所在平面上存在一点P，使它到三角形三个顶点的距离之和最小，则称点P为 Δ ABC的费马点，此时PA+PB+PC的值为 Δ ABC的费马距离．

    (2)、知识迁移

    ①我们有如下探寻 Δ ABC（其中∠A，∠B，∠C均小于120°）的费马点和费马距离的方法：

    如图2，在 Δ ABC的外部以BC为边长作等边三角形BCD及其外接圆，根据（1）的结论，易知线段的长度即为 Δ ABC的费马距离；

    ②在图3中，作出 Δ ABC(∠A=120°)的费马点P（要求尺规作图），若AB=AC=1，求出费马距离．

    (3)、知识应用

    如图4，在等腰直角三角形ABC中，∠B=90°，其费马距离为 6+2 ，求AB的长．

    查看试题解析